Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Это означает, что если вектор суммы (например, равнодействующая или главный вектор)

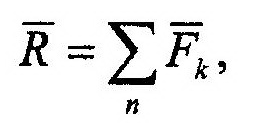
то, согласно выше сформулированной теореме проекции этого вектора можно определить как:

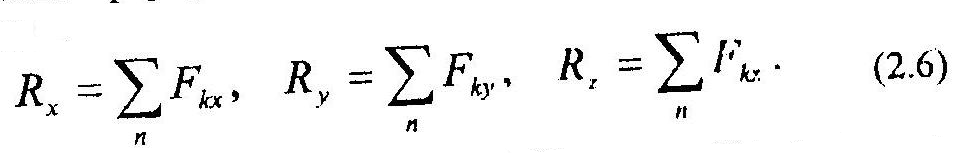
Таким образом, задача об аналитическом сложении сил сводится к нахождению проекций вектора суммы R по формулам (2.6) с последующим определением его модуля:

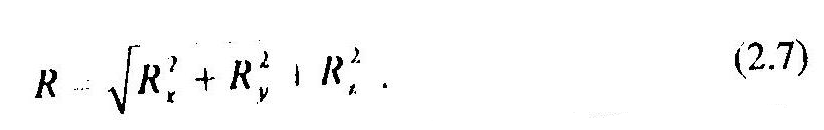
Направление искомого вектора R в пространстве определяют направляющие косинусы:

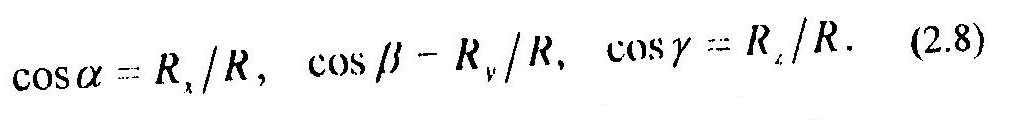
где α, β, γ – углы, которые образует вектор R с положительными направлениями осей x, y, z соответственно.

Равновесие системы сходящихся сил

Для равновесия ССС необходимо и достаточно, чтобы равнодействующая этих сил, R, была равна нулю.

Геометрическая интерпретация этого условия означает, что силовой многоугольник, построенный из этих сил(рис. 2.3), должен быть замкнутым.

В аналитической форме условие равновесия ССС может быть получено из выражения (2.7). Если R=0, то R_x=R_y=R_z=0. Учитывая, что R – это вектор суммы ССС, получим:

ΣF_kx=0, ΣF_ky=0, ΣF_kz=0 (2.9)

Условия (2.9) можно сформулировать следующим образом: