Естественный способ
| Данный способ используется в тех случаях, когда задана траектория точки. Для определения положения точки на траектории выбирается начало отсчета – точка О, относительно которой откладывается дуговая координата, S (рис. 8.2), и направление положительного отсчета S по траектории. Дуговая координата является условной скалярной величиной и может принимать как положительные, так и отрицательные значения. Однознач- | 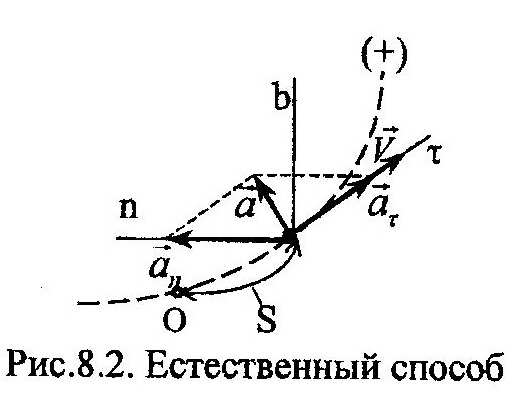
|
ная зависимость между S и временем, t, представляет собой уравнение движения точки в естественном способе задания движения:

Скорость точки, направленная по оси t, определяется как:

Ускорение точки, а, находится в плоскости nt и может быть разложено на составляющие:

Физический смысл этого разложения заключается в следующем: линия действия касательной составляющей, аt, совпадает с линией действия вектора скорости, V, и отражает изменение только модуля скорости; нормальная составляющая ускорения, аn, характеризует изменение направления линии действия вектора скорости. Их численные значения могут быть найдены по следующим формулам:
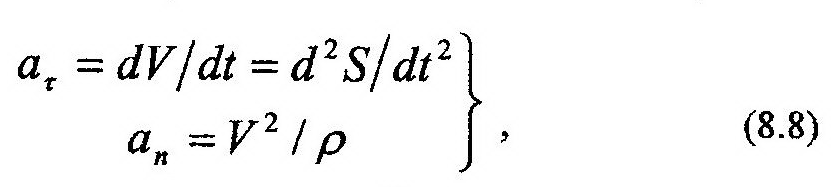
| где | 
| – радиус кривизны траектории в данной точке. |
Дата добавления: 2016-04-19; просмотров: 591;
