Теорема 4. Любая конечная игра размера m×n имеет решение, в котором число активных стратегий у каждого игрока не превосходит наименьшего из чисел m и n.

Из этой теоремы следует, что у игры размера 2×n всегда имеется решение, в котором каждый игрок использует не более двух активных стратегий.

Пользуясь геометрической интерпретацией, можно дать простой способ решения игры размера 2×n без седловой точки. Пусть платежная матрица игры имеет вид:

Для каждой из n чистых стратегий второго игрока строим график функции выигрыша первого игрока по формуле:

(1) ;

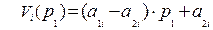Непосредственно по чертежу находим пару активных стратегий второго игрока, соответствующих двум графикам функций выигрыша, пересекающихся в точке с максимальной ординатой на нижней границе выигрышей и имеющих противоположные наклоны. Вместе со стратегиями первого игрока они образуют по теореме 4 игру размера 2×2, решение которой является решением и исходной игры.

Пример 3. Инга и Кора играют в следующую игру: Кора прячет в кулаке либо 1, либо 2, либо 3, либо 4 монеты (достоинством в 1 доллар). Инга угадывает: четное число монет или нечетное. Если она угадала, Кора отдает монеты, иначе Инга должна заплатить ту сумму, которая была в кулаке у Коры.

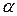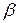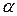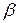Решение. Составим платежную матрицу игры размера 2×4 и найдем нижнюю и верхнюю цену игры. = –3 , = 1, < , следовательно, игра без седловой точки.

Кора Инга
чет	–1		–3		–3
нечет		–2		–4	–4

Функции выигрыша Инги, соответствующие чистым стратегиям Коры вычисляем по формуле (1):

Построим графики функций 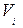на отрезке [0, 1] изменения частоты :

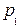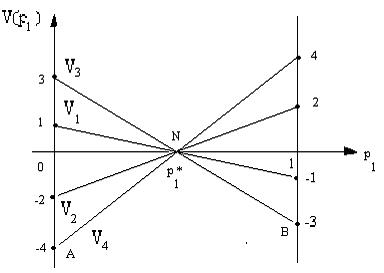
Рис. 9.2

Ломаная ANB является нижней границей выигрышей первого игрока, координаты точки N определяют оптимальную стратегию Инги и цену игры. Тока N – точка пересечения всех четырех графиков, в частности, и 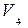с противоположными наклонами, поэтому активными стратегиями Коры можно считать третью и четвертую стратегии. Получаем игру размера 2×2 с платежной матрицей: , для которой находим, что = , 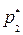= , V = 0, = , 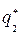= . Поэтому оптимальная стратегия Коры имеет вид:

.

Аналогично можно решить игру размера m×2, где m >2.