Теорема 2 (Неймана [19]): Каждая конечная игра имеет по крайней мере одно решение, возможно, среди смешанных стратегий.

Для нахождения решения конечных игр без седловой точки требуется ввести еще одно понятие «активной» стратегии:

Активной стратегией называется стратегия игрока, входящая в его смешанную стратегию с отличной от нуля частотой.

Теорема 3 (об активных стратегиях): если один из игроков придерживается своей оптимальной стратегии, то выигрыш остается неизменным и равным цене игры V, если другой игрок не выходит за пределы своих активных стратегий.

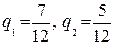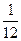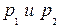Пример. Позднее мы докажем, что оптимальной стратегией Фионы в игре с пальцами является смешанная стратегия с частотами . Цена игры V = – . Так как игра без седловой точки, то обе стратегии Эдварда – активные. По теореме 3 при любых частотах стратегий Эдварда цена игры не изменится, если Фиона придерживается своей оптимальной стратегии. Пусть, например, частоты стратегий Эдварда таковы: 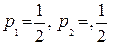. Средняя цена игры по формуле (1) равна: 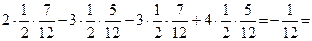V.

Теорема 3 имеет большое практическое значение, так как она в некоторых случаях позволяет найти решение игры без седловой точки.