Нижняя и верхняя цена игры. Принцип минимакса. Основные понятия теории игр
Элементы теории игр
Основные понятия теории игр
На практике часто приходится анализировать ситуации, в которых две или более стороны преследуют различные цели (в экономике, спорте, военном деле), причем результат любого действия, принятого каждой стороной, зависит от решений, которые принимают партнеры. В данной главе мы подробно рассмотрим ситуации, в которых участвуют две стороны, преследующие противоположные цели. Такие ситуации называют «конфликтными ситуациями».
Для анализа конфликтных ситуаций был разработан математический аппарат – теория игр. Теория игр – это математическая теория, исследующая ситуации, в которых принятие решений зависит от нескольких участников, и вырабатывающая рекомендации по рациональному образу действий каждого участника.
Игра – это формализованная модель реальной ситуации, описывающая действия двух или нескольких участников, выполняемые по определенным правилам. Примерами игр являются шахматы, футбол, карточные игры. Игра заканчивается выигрышем (победой) одного из игроков. Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Далее будем рассматривать только парные игры.
Игра называется игрой с нулевой суммой или антагонистической, если выигрыш одного из игроков равен проигрышу другого. В игре с нулевой суммой сумма выигрышей игроков всегда равна нулю.
Развитие игры во времени состоит из ряда последовательных этапов – «ходов» игроков. Ход игрока – это выбор одного из предусмотренных правилами игры действия игрока. Ходы делятся на случайные и личные. Случайный ход – это случайно выбранное действие, например, случайно выбранное число компьютером. Личный ход– это сознательный выбор игроком одного из возможных действий, например, выбор клетки в игре «крестики – нолики». Многие карточные игры относятся к играм смешанного типа, которые содержат как случайные, так и личные ходы, в отличие от шахмат, где все ходы – личные.
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся в игре ситуации. Если каждый из игроков имеет конечное число стратегий, то игра называется конечной. Если число стратегий хотя бы одного игрока бесконечно, то игра называется бесконечной.
Найти решение игры – это значит для каждого игрока выбрать стратегию, удовлетворяющую условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй игрок придерживается своей стратегии, и наоборот, второй игрок должен иметь минимальный проигрыш, когда первый игрок придерживается своей стратегии. Такие стратегии называются оптимальными. Оптимальные стратегии должны быть «устойчивыми», т.е. любому из игроков должно быть невыгодно отказаться от своей оптимальной стратегии.
Если игра повторяется многократно, то в качестве цены игры определяется средний выигрыш (математическое ожидание) первого игрока за одну игру.
Целью теории игр является определение оптимальной стратегии каждого из игроков. При этом предполагается, что оба игрока считают своего партнера таким же разумным, как и самого себя, следовательно, в теории игр не учитываются элементы риска, присутствующие в реальных ситуациях.
Рассмотрим парную антагонистическую конечную игру, в которой первый игрок имеет m стратегий, а второй игрок имеет n стратегий. Такая игра называется игрой размерности m×n. Пусть X = 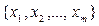 – множество стратегий первого игрока, Y =
– множество стратегий первого игрока, Y =  – множество стратегий второго игрока. В результате выбора игроками любой пары стратегий
– множество стратегий второго игрока. В результате выбора игроками любой пары стратегий 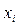 и
и 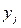 однозначно определяется выигрыш
однозначно определяется выигрыш  первого игрока или проигрыш
первого игрока или проигрыш 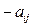 второго игрока. Предположим , что значения
второго игрока. Предположим , что значения 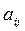 известны для любой пары стратегий
известны для любой пары стратегий 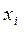 и
и 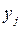 . Матрица A = (
. Матрица A = (  ), i = 1, 2, …, m; j = 1, 2, …, n, называется платежной матрицей или матрицей игры. Таким образом, любую конечную игру можно рассматривать как тройку объектов
), i = 1, 2, …, m; j = 1, 2, …, n, называется платежной матрицей или матрицей игры. Таким образом, любую конечную игру можно рассматривать как тройку объектов 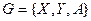 , где A – платежная матрица вида:
, где A – платежная матрица вида:
  Y
X Y
X
| 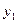
| 
| … | 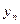
|
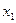
| 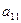
| 
| … | 
|
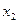
| 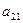
| 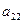
| … | 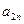
|
| … | … | … | … | … |
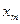
| 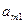
| 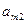
| … | 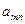
|
Пример1. Составим платежную матрицу для следующей игры: У Ани 2 карты – белая и черная с цифрой 1 на каждой. У Бори тоже 2 карты, черная с цифрой 1, а белая с цифрой 0. Цвет и цифры обозначены только на одной стороне, так что их можно скрыть от противника. Аня и Боря одновременно открывают одну из своих карт. Если цвета совпадают, то выигрывает Аня сумму (в рублях), равную разности показанных цифр. Если же карты разного цвета, то эту сумму получает Боря.
Решение. Если оба показывают белые карты, то Аня выигрывает 1 – 0 =1 рубль. Если обе карты черные, то выигрыш Ани равен 1– 1 =0.
Если у Ани белая карта, а у Бориса черная, то проигрыш Ани равен нулю. В противоположном случае она проигрывает 1 – 0 =1 рубль. Получаем платежную таблицу:
| Боря Аня | Б0 | Ч1 |
| Б1 | ||
| Ч1 | –1 |
Пример 2. Составим платежную матрицу для игры «Выбрасывание пальцев»: Эдвард и Фиона одновременно показывают друг другу один или два пальца. Если общее число показанных пальцев четное, то именно такую сумму в долларах выигрывает Эдвард. Если же было показано 3 пальца, то Фиона выигрывает 3 доллара.
Очевидно, у каждого из игроков имеется 2 стратегии – показать 1 или 2 пальца. Платежная таблица (выигрышей Эдварда) имеет вид:
| Фиона Эдвард | ||
| –3 | ||
| –3 |
Нижняя и верхняя цена игры. Принцип минимакса
Рассмотрим конечную игру  размерности m×n. Решим задачу: определить оптимальные стратегии игроков. Проанализируем каждую из стратегий первого игрока. Выбирая стратегию
размерности m×n. Решим задачу: определить оптимальные стратегии игроков. Проанализируем каждую из стратегий первого игрока. Выбирая стратегию 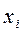 , он должен рассчитывать на то, что второй игрок ответит на нее той из своих стратегий
, он должен рассчитывать на то, что второй игрок ответит на нее той из своих стратегий 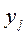 , для которой выигрыш первого игрока
, для которой выигрыш первого игрока  минимален. Обозначим это значение выигрыша
минимален. Обозначим это значение выигрыша 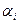 :
:
(1) 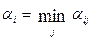 .
.
Здесь знаком 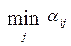 обозначено минимальное значение параметра
обозначено минимальное значение параметра  при всех возможных
при всех возможных 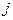 .
.
Выбирая какую–либо стратегию 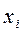 , первый игрок должен понимать, что в результате разумных действий противника он не выиграет больше, чем
, первый игрок должен понимать, что в результате разумных действий противника он не выиграет больше, чем 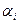 . Действуя осторожно и избегая всякого риска, он должен выбрать ту стратегию
. Действуя осторожно и избегая всякого риска, он должен выбрать ту стратегию 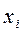 , для которой число
, для которой число 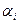 является максимальным. Обозначим это максимальное значение
является максимальным. Обозначим это максимальное значение 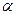 :
:
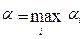 , или , учитывая формулу (1),
, или , учитывая формулу (1),
(2)  .
.
Величина 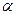 называется нижней ценой игры или максиминным выигрышем (максимином) первого игрока.
называется нижней ценой игры или максиминным выигрышем (максимином) первого игрока.
Число 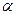 лежит в определенной строке платежной матрицы. Соответствующая этой строке стратегия первого игрока называется максиминной стратегией. Если он будет придерживаться максиминной стратегии, то ему при любом поведении противника гарантирован выигрыш не меньший
лежит в определенной строке платежной матрицы. Соответствующая этой строке стратегия первого игрока называется максиминной стратегией. Если он будет придерживаться максиминной стратегии, то ему при любом поведении противника гарантирован выигрыш не меньший 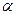 . Это его гарантированный выигрыш, если он придерживается наиболее осторожной максиминной стратегии.
. Это его гарантированный выигрыш, если он придерживается наиболее осторожной максиминной стратегии.
Аналогичное рассуждение можно провести за второго игрока. Так как он заинтересован в том, чтобы выигрыш первого игрока был минимальным, то он должен просмотреть каждую свою j–тую стратегию ( столбец чисел  ) и определить максимальный выигрыш первого игрока при этой стратегии. Обозначим это значение выигрыша
) и определить максимальный выигрыш первого игрока при этой стратегии. Обозначим это значение выигрыша 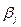 :
:
(3) 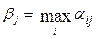 .
.
Выбирая какую–либо стратегию 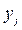 , второй игрок должен понимать, что в результате разумных действий противника он не проиграет больше, чем
, второй игрок должен понимать, что в результате разумных действий противника он не проиграет больше, чем  . Действуя осторожно и избегая всякого риска, он должен выбрать ту стратегию
. Действуя осторожно и избегая всякого риска, он должен выбрать ту стратегию  , для которой число
, для которой число  является минимальным. Обозначим это минимальное значение
является минимальным. Обозначим это минимальное значение 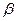 :
:
(4) 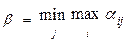
Величина 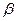 называется верхней ценой игры или минимаксным выигрышем (минимаксом) второго игрока.
называется верхней ценой игры или минимаксным выигрышем (минимаксом) второго игрока.
Соответствующая столбцу с числом 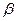 стратегия второго игрока называется его минимаксной стратегией. Если он будет придерживаться своей минимаксной стратегии, то ему при любом поведении первого игрока гарантирован проигрыш не больший
стратегия второго игрока называется его минимаксной стратегией. Если он будет придерживаться своей минимаксной стратегии, то ему при любом поведении первого игрока гарантирован проигрыш не больший 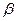 .
.
Принцип осторожности, диктующий игрокам выбор своих наиболее осторожных стратегий (максиминной для первого и минимаксной для второго игроков) в теории игр называется «принципом минимакса». Максиминную и минимаксную стратегии игроков обозначают общим термином «минимаксные стратегии».
В качестве примеров определим нижнюю и верхнюю цену игры и минимаксные стратегии для примеров 1, 2 из предыдущего раздела.
Пример 1. Игра Ани и Бори. Добавим к платежной матрице игры справа столбец чисел 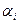 и снизу строку чисел
и снизу строку чисел  :
:
| Боря Аня | Б0 | Ч1 | 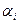
|
| Б1 | |||
| Ч1 | –1 | –1 | |

|
Вычисляем нижнюю цену игры по формуле (2): 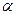 = 0, верхнюю цену игры по формуле (4):
= 0, верхнюю цену игры по формуле (4): 
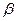 = 0. Они оказались одинаковыми.
= 0. Они оказались одинаковыми.
Элемент 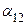 = 0, выделенный в платежной матрице, является одновременно минимальным в строке и максимальным в столбце. В геометрии точку на поверхности, обладающую свойством: аппликата точки минимальна по одной координате и максимальна по другой, называют седловой точкой. По аналогии этот термин применяется в теории игр: элемент платежной матрицы с указанным свойством называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.
= 0, выделенный в платежной матрице, является одновременно минимальным в строке и максимальным в столбце. В геометрии точку на поверхности, обладающую свойством: аппликата точки минимальна по одной координате и максимальна по другой, называют седловой точкой. По аналогии этот термин применяется в теории игр: элемент платежной матрицы с указанным свойством называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.
Если нижняя цена игры равна верхней, то их общее значение называется ценой игры (иногда – чистой ценой игры).
Седловой точке соответствует пара минимаксных стратегий. В примере 1 – это стратегии 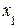 и
и 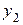 . Они являются оптимальными стратегиями игроков. Если один из игроков, например, Боря, отклонится от своей оптимальной второй стратегии, а Аня будет придерживаться своей первой оптимальной стратегии, то Боря проиграет 1 рубль. Таким образом, решением игры Ани и Бори является пара их минимаксных стратегий.
. Они являются оптимальными стратегиями игроков. Если один из игроков, например, Боря, отклонится от своей оптимальной второй стратегии, а Аня будет придерживаться своей первой оптимальной стратегии, то Боря проиграет 1 рубль. Таким образом, решением игры Ани и Бори является пара их минимаксных стратегий.
Для каждой игры с седловой точкой существует решение – пара минимаксных стратегий игроков, являющиеся оптимальными стратегиями игроков , а цена игры v равна общему значению нижней и верхней цены игры: v = 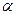 =
= 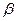 . Это решение обладает свойством:
. Это решение обладает свойством:
Если один из игроков придерживается своей оптимальной стратегии, а другой отклоняется от своей оптимальной стратегии, то от этого он может только потерять и ни в коем случае не увеличить свой выигрыш.
Пример 2. Игра Эдварда и Фионы. Снова добавим к платежной матрице игры справа столбец чисел 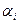 и снизу строку чисел
и снизу строку чисел  . Вычисляем нижнюю цену игры по формуле (2):
. Вычисляем нижнюю цену игры по формуле (2): 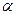 = –3 , верхнюю цену игры по формуле (4):
= –3 , верхнюю цену игры по формуле (4): 
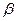 = 2. Они оказались неодинаковыми. Заметим, что
= 2. Они оказались неодинаковыми. Заметим, что 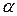 <
< 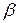 , игра не имеет седловой точки.
, игра не имеет седловой точки.
| Фиона Эдвард | 
| ||
| –3 | –3 | ||
| –3 | –3 | ||
 
|
Теорема 1. Для любой конечной игры выполняется неравенство:
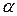 £
£ 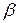
Доказательство. Пусть 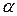 =
= 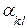 ,
, 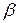 =
= 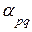 По определению чисел
По определению чисел 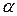 и
и 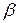 имеем:
имеем: 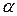 £
£  ,
, 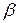 ³
³  , следовательно,
, следовательно, 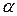 £
£ 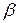 .
.
Для первого игрока в примере 2 любая стратегия является максиминной, для второго игрока минимаксной стратегией является его первая стратегия.
В случае 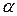 <
< 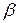 , как в примере 2, минимаксные стратегии игроков являются неустойчивыми. В самом деле, пусть первый игрок применяет свою первую максиминную стратегию, а второй – свою минимаксную первую стратегию. До тех пор, пока оба игрока придерживаются этих стратегий, выигрыш первого игрока равен 2. Но если второму игроку станет известно, что первый игрок применяет первую стратегию, то он применит свою вторую стратегию и сведет выигрыш противника к –3. Наоборот, если первому игроку станет известно, что второй игрок применяет вторую стратегию, то он применит тоже вторую стратегию и увеличит свой выигрыш до 4. Поэтому минимаксные стратегии игроков в игре без седловой точки не являются оптимальными.
, как в примере 2, минимаксные стратегии игроков являются неустойчивыми. В самом деле, пусть первый игрок применяет свою первую максиминную стратегию, а второй – свою минимаксную первую стратегию. До тех пор, пока оба игрока придерживаются этих стратегий, выигрыш первого игрока равен 2. Но если второму игроку станет известно, что первый игрок применяет первую стратегию, то он применит свою вторую стратегию и сведет выигрыш противника к –3. Наоборот, если первому игроку станет известно, что второй игрок применяет вторую стратегию, то он применит тоже вторую стратегию и увеличит свой выигрыш до 4. Поэтому минимаксные стратегии игроков в игре без седловой точки не являются оптимальными.
В случае игры без седловой точки неясно, как находить цену игры и как определять оптимальные стратегии. Для этого необходимо обобщить понятие стратегии, определив понятие смешанной стратегии, предложенной Д. Бернулли в 1732 году.
Дата добавления: 2016-04-14; просмотров: 29987;
