Постановка задачи целочисленного программирования
Некоторые задачи линейного программирования требуют целочисленного решения. К ним относятся задачи по производству и распределению неделимой продукции (выпуск станков, телевизоров, автомобилей и т.п.). Математическая модель задачи целочисленного программирования имеет вид:
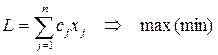
при ограничениях:
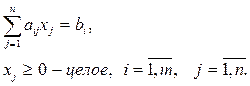
Оптимальное решение, найденное симплексным методом, часто не является целочисленным. Его можно округлить до ближайших целых чисел. Однако такое округление может дать решение, не лучшее среди целочисленных решений, или привести к решению, не удовлетворяющему системе ограничений. Поэтому для нахождения целочисленного решения нужен особый алгоритм, например, алгоритм Гомори.
Пример. Прогнозирование эффективного использования производственных площадей
Постановка задачи
В целях улучшения финансового положения фирма приняла решение об увеличении выпуска конкурентоспособной продукции. Для этого решено было установить в одном из цехов дополнительное оборудование, занимающее 19/3 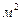 площади. На приобретение дополнительного оборудования фирма выделила 10 усл. ед. При этом она может купить оборудование двух видов. Приобретение 1-го комплекта оборудования 1-го вида стоит 1.0 усл. ед., 2-го вида – 3 усл. ед. Приобретение одного комплекта оборудования 1-го вида позволяет увеличить выпуск продукции в смену на 2 шт., а одного комплекта оборудования 2-го вида – на 4 шт. Зная, что для установки одного комплекта оборудования 1-го вида требуется 2
площади. На приобретение дополнительного оборудования фирма выделила 10 усл. ед. При этом она может купить оборудование двух видов. Приобретение 1-го комплекта оборудования 1-го вида стоит 1.0 усл. ед., 2-го вида – 3 усл. ед. Приобретение одного комплекта оборудования 1-го вида позволяет увеличить выпуск продукции в смену на 2 шт., а одного комплекта оборудования 2-го вида – на 4 шт. Зная, что для установки одного комплекта оборудования 1-го вида требуется 2 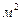 площади, а для оборудования 2-го вида – 1
площади, а для оборудования 2-го вида – 1 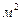 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции.
площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции.
Составим математическую модель задачи. Предположим, что фирма приобретает 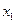 комплектов дополнительного оборудования 1-го типа и
комплектов дополнительного оборудования 1-го типа и 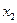 комплектов оборудования 2-го типа. Тогда целевая функция имеет вид:
комплектов оборудования 2-го типа. Тогда целевая функция имеет вид:
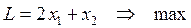
при ограничениях
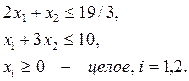
Дата добавления: 2016-04-14; просмотров: 906;
