Постановка задачи линейного программирования
Линейное программирование
Краткая характеристика пакета Qmwin
Пакет Qmwin (quantitative methods for Windows – количественные методы для Windows) версии 1.03.06.05 (1996 г., автор Howard J. Weiss) предназначен для решения задач исследования операций. Пакет имеет 18 разделов, посвященных различным областям исследования операций:
1. Прогнозирование (Forecasting).
2. Принятие (анализ) решений (Decision Analysis).
3. Анализ ценообразования (Breakeven / Cost-Volume Analysis).
4. Управление качеством (Quality Control).
5. Инвентаризация (Inventory).
6. Планирование материальных потребностей (Material Requirements Planning).
7. Линейное программирование (Linear Programming).
8. Транспортные задачи (Transportation).
9. Задачи о назначениях (Assignment).
10. Целочисленное программирование (Integer Programming).
11. Смешанное целочисленное программирование (Mixed (and 0/1) Integer Programming).
12. Целевое программирование (Goal Programming).
13. Системы массового обслуживания (Waiting Lines).
14. Моделирование (Simulation).
15. Сетевые модели (Networks models).
16. Управление проектом (Project Management).
17. Марковский анализ (Markov Analysis).
18. Теория игр (Game Theory).
Методические указания
Постановка задачи линейного программирования
Задача линейного программирования является простейшим случаем математического программирования. Практические задачи, решаемые методами линейного программирования, характеризуются следующими общими чертами:
1. Решением задачи является ряд неотрицательных переменных 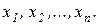
2. Решение задачи должно удовлетворять некоторым ограничениям в виде равенств или неравенств относительно переменных 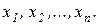
3. Решение задачи должно обращать в минимум (максимум) некоторую линейную функцию 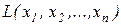 тех же переменных, которую обычно называют целевой функцией.
тех же переменных, которую обычно называют целевой функцией.
Заметим, что решение в данном случае нельзя найти, как это принято в математике, просто продифференцировав 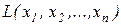 по ее аргументам. Действительно, так как функция
по ее аргументам. Действительно, так как функция 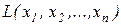 линейна, то производные от нее по всем аргументам постоянны и нигде в нуль не обращаются. Минимум (максимум) функции
линейна, то производные от нее по всем аргументам постоянны и нигде в нуль не обращаются. Минимум (максимум) функции 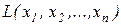 , если он существует, достигается всегда где-то на границе области возможных значений
, если он существует, достигается всегда где-то на границе области возможных значений 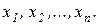 Математический аппарат линейного программирования позволяет последовательно обследовать границы области возможных решений и найти на этих границах то решение, которое является оптимальным, т.е. такую совокупность значений
Математический аппарат линейного программирования позволяет последовательно обследовать границы области возможных решений и найти на этих границах то решение, которое является оптимальным, т.е. такую совокупность значений 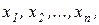 при которой линейная функция
при которой линейная функция 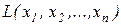 обращается в минимум (максимум).
обращается в минимум (максимум).
Выделяют так называемую основную задачу линейного программирования (ОЗЛП), на которую ориентированы известные методы решения и к которой сводятся другие варианты постановки задачи. Приведем ее формулировку.
Имеется ряд переменных 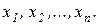
Требуется найти такие неотрицательные значения этих переменных, которые удовлетворяли бы системе линейных уравнений:
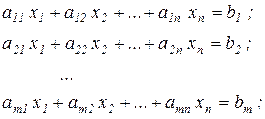 (1)
(1)
и, кроме того, обращали бы в минимум линейную функцию
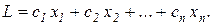 (2)
(2)
Одним из методов решения основной задачи линейного программирования является симплекс-метод.
Однако далеко не любая задача линейного программирования совпадает с ОЗЛП. Так, например, может потребоваться обращение функции 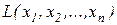 не в минимум, а в максимум или ограничения могут быть полностью или частично заданы в виде неравенств. Покажем, как в этих случаях можно перейти к ОЗЛП.
не в минимум, а в максимум или ограничения могут быть полностью или частично заданы в виде неравенств. Покажем, как в этих случаях можно перейти к ОЗЛП.
Случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к ОЗЛП. Для этого достаточно изменить знак функции и рассмотреть вместо нее функцию
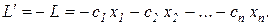
Пусть теперь имеется задача линейного программирования, в которой ограничения имеют вид линейных неравенств. В некоторых из них знак неравенства может быть 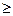 , а в других
, а в других 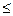 . Приведем все ограничения к стандартному виду (путем изменения знака обеих частей там, где это требуется):
. Приведем все ограничения к стандартному виду (путем изменения знака обеих частей там, где это требуется):
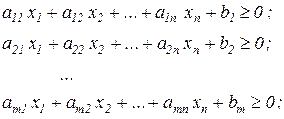 (3)
(3)
Введем новые переменные 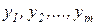 , которые называют добавочными:
, которые называют добавочными:
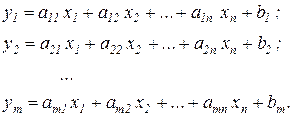 (4)
(4)
Эти переменные в силу (3) должны быть неотрицательны. В результате возникает ОЗЛП в следующей постановке. Найти такие неотрицательные значения 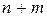 переменных
переменных 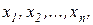
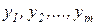 , чтобы они удовлетворяли ограничениям (4) и одновременно обращали в минимум функцию (2).
, чтобы они удовлетворяли ограничениям (4) и одновременно обращали в минимум функцию (2).
Пример. Выбор оптимального варианта выпуска изделий
Постановка задачи
Пусть фирма выпускает два вида мороженого: сливочное и шоколадное 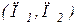 с розничной ценой за 1 кг соответственно
с розничной ценой за 1 кг соответственно 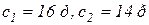 . Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы
. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы 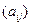 которых на
которых на
1 кг мороженого и суточные запасы приведены в таблице.
| Молоко | Наполнители | |
Сливочное ( 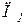 ) )
| 0,8 | 0,4 |
Шоколадное ( 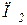 ) )
| 0,5 | 0,8 |
| Запас (кг) |
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?
Обозначим переменными 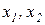 искомые количества продуктов
искомые количества продуктов 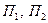 соответственно. Тогда целевая функция, которой, очевидно, является доход фирмы, имеет вид:
соответственно. Тогда целевая функция, которой, очевидно, является доход фирмы, имеет вид:
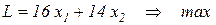 .
.
При этом ограничения по запасам и спросу имеют вид:
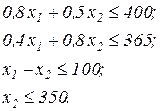
Дата добавления: 2016-04-14; просмотров: 803;
