Задачи для самостоятельного решения. 1. Пять человек должны выполнить четыре работы, причем каждый из работников с разной производительностью может выполнить любую из этих работ
1. Пять человек должны выполнить четыре работы, причем каждый из работников с разной производительностью может выполнить любую из этих работ. Предполагается, что каждый работник в состоянии сделать только одну работу. Производительности работников заданы таблицей:
| Работы | Работники | ||||
Распределить людей на работу так, чтобы выполнить ее с максимальной производительностью.
2. Фирма, имеющая четыре склада, получила четыре заказа, которые необходимо доставить различным потребителям. Складские помещения каждой базы имеют вполне достаточное количество товара, чтобы выполнить любой один из этих заказов. Расстояние между каждой базой и каждым потребителем приведены в таблице:
| Заказы | Базы | |||
Как следует распределить заказы по базам, чтобы общая дальность транспортировки была минимальной?
3. Фирма объединяет три предприятия, каждое из которых производит три вида изделий. Себестоимости каждого изделия в усл. ед. при изготовлении на каждом предприятии указаны в таблице:
| Изделия | Предприятия | ||
Учитывая необходимость специализации каждого предприятия только по одному изделию, распределить производство изделий по предприятиям так, чтобы изделия имели минимальную себестоимость.
4. Компания вырабатывает план выпуска трех новых видов продукции. Она уже владеет пятью предприятиями, и теперь на трех из них должны производиться новые виды продукции – по одному виду на одно предприятие.
Даны издержки производства единицы продукции (усл. ед.):
| Вид продукции | Предприятия | ||||
Кроме того, известны издержки сбыта единицы продукции (усл. ед.):
| Вид продукции | Предприятия | ||||
Плановый объем годового производства, который позволил бы удовлетворить спрос, и себестоимость единицы продукции каждого вида приведены в таблице:
| Вид продукции | Плановый объем производства, шт. | Себестоимость, усл. ед. |
Закрепить выпуск продукции между предприятиями, обеспечивающий получение наибольшей прибыли за год.
Лабораторная работа № 5
Тема: Управления проектом
Цель: научиться решать прикладные экономические задачи управления проектом с использованием пакета прикладных программ Qmwin.
Методические указания
Постановка задачи сетевого планирования
Задача управления проектом – это задача планирования комплекса работ, который состоит из ряда отдельных элементарных работ. Эти работы не просто выполняются независимо друг от друга, а взаимно обуславливают друг друга так, что выполнение некоторых одних работ не может быть начато раньше, чем закончатся некоторые другие. Например, при строительстве промышленного объекта закладка фундамента не может начаться раньше окончания рытья котлована, а рытье котлована не может начаться раньше окончания строительства подъездных путей и т.д. Планирование любого такого комплекса работ должно производиться с учетом времени, требующегося для выполнения работ, стоимости всех работ, сырьевых, энергетических и людских ресурсов.
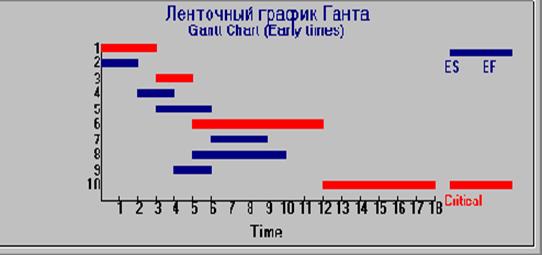
Результатом планирования работ является сетевая модель или ленточный график Ганта. Сетевая модель (сетевой график) – это ориентированный граф без контуров. Его основными элементами являются работа, обычно представляемая ребром, и событие, связанное с окончанием одной или нескольких работ, которое обычно представляется вершиной. Ленточный график Ганта строится над осью времени и представляет собой множество отрезков полос (ленточек), каждый из которых отмечает интервал времени, отводимый для исполнения некоторой работы. Ленточки упорядочены в соответствии с последовательностью исполнения соответствующих работ. Сетевой график является более наглядным представлением плана работ, однако ниже рассматривается график Ганта, т.к. он используется в пакете Qmwin.
Работа – это активный процесс, требующий затрат ресурсов, либо пассивный (ожидание).
Критическая последовательность работ – это последовательность, не имеющая резервов времени. Работы, принадлежащие критической последовательности, называются критическими. В сетевом графике критическая последовательность работ называется критическим путем.
Процедуры построения сетевого графика и графика Ганта во многом аналогичны. В их основе лежит структурная таблица, имеющая два столбца и описывающая существующую между работами зависимость. Каждая строка таблицы соответствует некоторой работе. При этом в одном столбце размещено имя этой работы, а в другом имена работ, на которые данная работа опирается. Строки этой таблицы упорядочиваются с использованием специального правила ранжирования работ. Работа называется работой первого ранга, если для ее начала не требуется выполнения никаких других работ. Работа называется работой k-го ранга, если для ее начала требуется выполнение работ не выше (k-1)-го ранга и среди этих работ имеется хотя бы одна работа (k-1)-го ранга. Полученная таблица достраивается до структурно-временной таблицы добавлением столбца с временами выполнения для всех работ.
По упорядоченной структурно-временной таблице строится как сетевой график, так и график Ганта. Формальный алгоритм построения опирается на описание этой таблицы в виде математических формул, отражающих связи между работами. Для этого обозначим 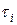 – минимально возможный срок начала работы
– минимально возможный срок начала работы 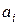 (время, отсчитываемое от начала процесса), а
(время, отсчитываемое от начала процесса), а 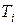 – минимально возможный срок ее окончания. Очевидно:
– минимально возможный срок ее окончания. Очевидно:
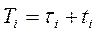 ,
,
где 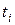 – время выполнения работы
– время выполнения работы 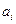 .
.
Пользуясь этими обозначениями, можно записать формулами все логические связи между работами комплекса. Действительно, пусть, например, работа 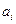 опирается на работы
опирается на работы 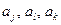 . Тогда работа
. Тогда работа 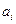 не может начаться раньше, чем кончится та из работ
не может начаться раньше, чем кончится та из работ 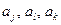 , которая кончается позже всех. Эту связь можно записать в виде формулы:
, которая кончается позже всех. Эту связь можно записать в виде формулы:
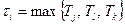 . (1)
. (1)
Применяя такие формулы ко всем работам комплекса по очереди, можно найти моменты окончания 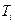 для всех работ и в конце концов, минимальный срок окончания всего комплекса работ
для всех работ и в конце концов, минимальный срок окончания всего комплекса работ 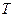 .
.
Чтобы найти критические работы, а стало быть и критический путь, нужно сделать следующее. Прежде всего, найти работу 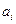 , для которой время окончания максимально, т.е.
, для которой время окончания максимально, т.е. 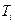 =
= 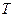 . Эта работа, конечно, будет критической. Затем следует среди формул (1) найти ту, которой определяется момент начала этой работы
. Эта работа, конечно, будет критической. Затем следует среди формул (1) найти ту, которой определяется момент начала этой работы 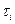 . Величина
. Величина 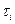 представлена в виде максимума каких-то моментов
представлена в виде максимума каких-то моментов 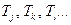 . Нужно найти тот из них, на котором достигается максимум (если таких моментов несколько, то взять любой). Та работа
. Нужно найти тот из них, на котором достигается максимум (если таких моментов несколько, то взять любой). Та работа 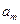 , при которой достигается максимум, будет второй от конца работой на критическом пути. Далее точно также определяется третья и т.д. работы на критическом пути. Поскольку максимум в каких-нибудь из формул может достигаться не на одной, а на нескольких работах, то в результате могут быть получены несколько критических путей.
, при которой достигается максимум, будет второй от конца работой на критическом пути. Далее точно также определяется третья и т.д. работы на критическом пути. Поскольку максимум в каких-нибудь из формул может достигаться не на одной, а на нескольких работах, то в результате могут быть получены несколько критических путей.
Стоимостные факторы при реализации плана учитываются путем определения зависимости «продолжительность – затраты» для каждой работы. Продолжительность работы можно уменьшить, увеличив интенсивность использования ресурсов, а, следовательно, увеличив стоимость работы. Обычно из соображений удобства принимается линейная зависимость «продолжительность – затраты», т.к. ее аналитическое описание можно определить по двум точкам нормального и максимально интенсивного режимов. Пусть 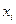 – это затраты, дополнительно отпускаемые на реализацию работы
– это затраты, дополнительно отпускаемые на реализацию работы 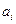 . Тогда линейная зависимость «продолжительность - затраты» имеет вид:
. Тогда линейная зависимость «продолжительность - затраты» имеет вид:
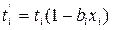 ,
,
где 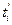 – новое значение продолжительности работы.
– новое значение продолжительности работы.
Чтобы добиться некоторого сокращения общей продолжительности работ при минимально возможных затратах, необходимо в максимальной степени сжать ту критическую работу, у которой наклон прямой «продолжительность – затраты» наибольший. В результате сжатия критической работы получается новый план с, возможно, новым критическим путем. Стоимость работ при этом будет выше. На следующем этапе можно сжимать другие критические работы.
Можно задачу оптимизации плана поставить по другому, а именно, потребовать сокращения длины критического пути и, как следствие, возможно, (если критический путь не измениться) и общей продолжительности работ не менее чем до заданного значения 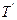 , при минимальных дополнительных затратах. Математическая постановка задачи при этом имеет вид:
, при минимальных дополнительных затратах. Математическая постановка задачи при этом имеет вид:
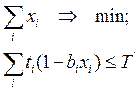
В обоих суммах суммирование производится по работам критического пути.
Пример. План создания нового бытового прибора
Расчет временных параметров плана
Пусть работы, необходимые для создания нового бытового прибора описываются следующей структурно-временной таблицей.
| Работа | Содержание работы | Непосредственно предшествующие работы | Продолжительность |
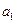
| Разработка технической документации на прибор. | ||
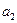
| Разработка технической документации на электронную часть прибора. | ||
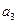
| Разработка технологической документации на прибор. | 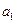
| |
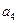
| Разработка технологической документации на электронную часть прибора. | 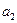
| |
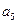
| Передача технической документации на прибор. | 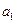
| |
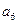
| Изготовление прибора | 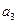
| |
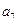
| Изготовление электронной части прибора. | 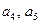
| |
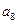
| Разработка эксплуатационной технической документации на прибор. | 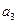
| |
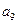
| Разработка эксплуатационной технической документации на электронную часть прибора. | 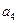
| |
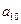
| Сборка и испытание прибора | 
|
Основным временным параметром плана работ является продолжительность критической последовательности работ (критического пути). Определим этот параметр для рассматриваемого примера. Имеем:
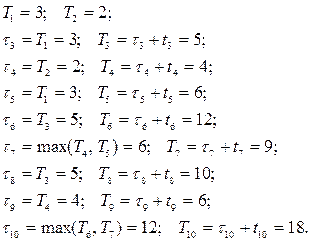
Время выполнения всего комплекса работ есть максимальное из всех времен 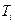 , т.е.
, т.е.
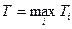 .
.
В данном случае 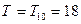 .
.
Найдем критические работы, начиная с последней. Так как максимум достигается для 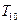 , то работа
, то работа 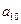 является критической. Она опирается на работы
является критической. Она опирается на работы 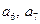 , из которых
, из которых 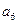 является критической, поскольку имеет наибольшую в этой паре работ длительность. Работа
является критической, поскольку имеет наибольшую в этой паре работ длительность. Работа 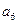 опирается только на
опирается только на 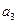 , поэтому
, поэтому 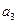 также критическая работа. Работа
также критическая работа. Работа 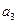 опирается только на
опирается только на 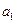 , поэтому и
, поэтому и 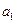 – критическая работа. Таким образом критическая последовательность работ (критический путь) состоит из
– критическая работа. Таким образом критическая последовательность работ (критический путь) состоит из 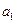 ,
, 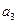 ,
, 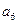 и
и 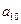 .
.
После определения критического пути можно построить сетевой график или график Ганта. Сначала над осью времени последовательно друг за другом отображаются критические работы, а затем критический путь дополняется всеми остальными работами. График Ганта, соответствующий рассмотренному примеру, представлен на рисунке в начале описания.
Дата добавления: 2016-04-14; просмотров: 2296;
