Постановка задачи при стратегической игре

Игра – это упрощенная формализованная модель реальной конфликтной ситуации. Математическая формализация в данном случае означает, что выработаны определенные правила действия сторон в процессе игры:

- варианты действия сторон;

- исход игры при данном варианте действия;

- объем информации для каждой стороны о поведении всех других сторон.

Выигрыш или проигрыш сторон (критерий качества действий) оценивается численно.

Игрок – это одна из сторон в игровой ситуации.

Стратегия игрока – это его правила действия в каждой из возможных ситуаций игры.

Содержание игры описывается с помощью платежной матрицы (матрицы эффективности), которая включает все значения выигрышей. Пусть в игре участвуют два игрока, и первый игрок имеет 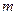(чистых) стратегий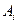 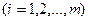, а второй игрок – 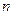(чистых) стратегий 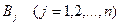. Тогда игра называется игрой 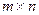для двух игроков. Если число стратегий у каждого из игроков конечно, то игра называется конечной, в противном случае – бесконечной. Игры подразделяются на игры с нулевой суммой, когда сумма выигрышей всех игроков в каждой партии равна нулю, и игры с ненулевой суммой – в противном случае. Различают одношаговые и многошаговые игры. Одношаговые игры заканчиваются после одного шага каждого игрока. Конечная игра двух игроков с нулевой суммой называется матричной игрой, а платежная матрица в этом случае имеет вид:

Таблица 1

Игрок 1   Игрок 2			…
			…
			…
…	…	…	…	…	…
			…
			…

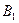
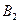
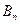
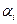
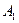
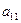
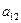
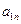
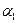
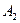
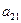
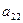
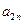
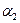
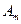
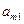
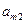
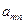
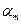
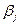
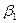
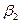
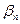
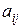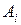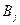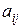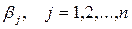В данной матрице элементы – значения выигрышей игрока 1 в случае, когда он использует стратегию , а игрок 2 использует стратегию . При этом выигрыш (проигрыш) игрока 2 равен (- ), поскольку игра с нулевой суммой. Величины и отражают в матрице соответственно минимальные значения элементов 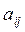по строкам и максимальные – по столбцам.

Рассмотрим одношаговую игру, представленную платежной матрицей (табл. 1). Содержанием игры является выбор стратегии за игрока 1. Будем считать, что игра выполняется только один раз и надо решить, какую стратегию выбрать из заданного множества чистых стратегий { 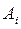| 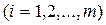}. Очевидно, что исход игры случаен, и невозможно предсказать значение выигрыша для первого игрока. Однако пусть игрок 1 выберет среди существующих стратегию с особыми свойствами, которая называется максиминной. Тогда значение выигрыша будет принадлежать интервалу, в общем случае существенно меньшему, нежели исходный интервал, заданный содержанием платежной матрицы. Этот интервал, как и всякий интервал, будет характеризоваться нижней и верхней границами, которые называются соответственно нижней и верхней границами игры. В основе максиминного подхода к решению игры лежит предположение о том, что игрок 2, по меньшей мере, так же разумен, как и игрок 1 и делает все возможное, чтобы помешать игроку 1 добиться своей цели. Таким образом, игрок 1 должен рассчитывать на худшие условия (на самый «неприятный» ход со стороны игрока 2). Этот подход формулируется в виде принципа «максимина» как получение максимального результата при наихудших условиях. Уточним этот подход.

Подход игрока 1. Сначала для каждой стратегии 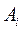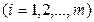следует определить минимальный выигрыш (наихудшее условие):

.

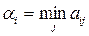Очевидно, что, выбирая конкретную стратегию 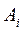, игрок может рассчитывать, что с гарантией получит только выигрыш 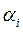. Следующий шаг очевиден. Среди возможных стратегий следует предпочесть ту, у которой число 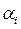максимально, т.е.:

.

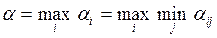Величина 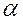называется нижней ценой игры, иначе максиминным выигрышем или максимином. Та стратегия 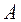, которая соответствует максимину 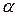, называется максиминной стратегией. При ее использовании игрок 1 получает выигрыш не меньше .

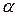Подход игрока 2. При обсуждении поведения игрока 2 необходимо продолжать следовать осторожной логике рассматриваемого подхода, предполагающего для него ту же степень разумности, что и для игрока 1. Как вскоре будет показано, это приводит к тому, что игроку 1 в общем случае не приходится рассчитывать на максимальный выигрыш, предусмотренный в платежной матрице. Итак, игрок 2, следуя той же логике, что и игрок 1, должен для каждой стратегии 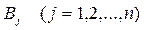определить минимальный выигрыш. Однако операции осуществляются над платежной матрицей, где проставлены выигрыши для игрока 1, а для него в этом случае выигрыш будет максимальным. В связи с этим, определяя наихудшие условия, надо для каждой стратегии игрока 2 определить максимальное значение выигрыша игрока 1:

.

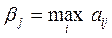Далее, следуя логике подхода, из всех стратегий выбирается та, для которой число 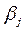минимально, т.е.:

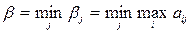
Величина 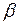называется верхней ценой игры или минимаксным выигрышем, или минимаксом. Соответствующая выигрышу 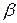стратегия противника называется его минимаксной стратегией. Придерживаясь минимаксной стратегии, противник гарантирован, что в любом случае проиграет не больше 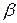. Однако и игрок 1 должен смириться с тем, что при таких предположениях не выиграет больше 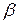. В реальности выигрыш может превысить 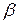, если игрок 2 не придерживается минимаксной стратегии. Максиминную и минимаксную стратегии часто обозначают общим термином «минимаксные стратегии». Принцип осторожности, диктующий игрокам выбор максиминной и минимаксной стратегий, является в теории игр основным и называется принципом минимакса.

Если игроки играют один раз, то принцип минимакса является хорошим руководством к действию. Ситуация меняется, если игра повторяется и игроки знают стратегии, использованные противником на предыдущих шагах, а значит, могут скорректировать свое поведение, изменив стратегию. В одних играх отклонение от минимаксных стратегий может оказаться выгодным, в других – нет. Про последние говорят, что эти игры имеют седловую точку. Определяющим признаком седловой точки является равенство нижней и верхней оценок игры.

В результате оказывается, что даже, если игрок знает стратегию противника, он не будет отклоняться от минимакса, т.к. ему это не выгодно. В этом случае говорят о чистой цене игры

.

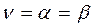Седловой точке соответствует пара минимаксных стратегий, которые называются оптимальными или решением игры.

Среди игр, имеющих практическое значение, не так уж часто встречаются игры с седловой точкой, когда принцип минимакса является оправданной рекомендацией. При отсутствии седловой точки отсутствуют и мотивы, удерживающие игроков в рамках минимаксных стратегий. Однако с отклонением от них исчезает и гарантия минимаксного выигрыша. Напомним, что до сих пор варианты действий игроков ограничивались списком чистых стратегий. Возникает вопрос: нельзя ли гарантировать выигрыш больший 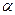, если применять не одну чистую стратегию, а чередовать случайным образом несколько стратегий. Такие стратегии называются смешанными. При использовании смешанной стратегией перед каждой партией игры пускается в ход какой-то механизм случайного выбора (бросание монеты, игральной кости, вычисление машиной случайного числа). При этом выбирается та стратегия, на которую пал жребий. В результате тактика становится более гибкой и противник не знает заранее, с какой обстановкой ему придется встретиться.

Пусть имеется игра 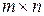. Тогда будем задавать смешанную стратегию 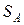игрока 1 следующим образом:

,

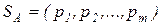где стратегия 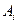применяется с вероятностью .

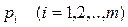Причем:

.

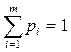Аналогично для смешанной стратегии 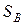игрока 2 имеем:

, .

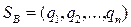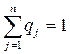Очевидно, что любая чистая стратегия является частным случаем смешанной, когда одна вероятность равна единице, а все остальные нулю.

Оказывается, если допустить не только чистые, но и смешанные стратегии, то можно для каждой конечной игры найти решение, т.е. пару устойчивых оптимальных стратегий игроков (основная теорема теории игр). Оптимальные стратегии обладают следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому не может быть выгодно отступать от своей. В этом случае игра имеет цену 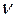, которая лежит между нижней и верхней ценами игры:

.

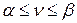Выгодность той или иной смешанной стратегии уже оценивается с точки зрения среднего выигрыша (математического ожидания выигрыша):

.

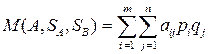При этом верхняя и нижняя цены определяются выражениями:

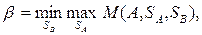
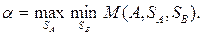
Определим решение в наиболее простом случае игры 2х2, когда седловая точка отсутствует, т.е. найдем оптимальную смешанную стратегию. В этом случае с учетом 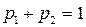, имеем:

.

.

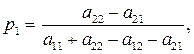
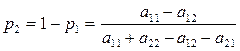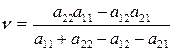Оптимальную смешанную стратегию можно найти графическим методом. Для этого воспользуемся выражениями для выигрышей игрока 1 в двух случаях, когда игрок 2 использует стратегию 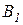и когда он использует стратегию :

.

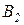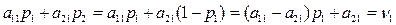
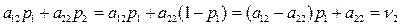Эти выражения описывают линейную зависимость среднего выигрыша 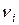при стратегии игрока 2 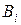. Каждая из этих зависимостей в осях ( 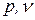) представляется соответствующей прямой. Пересечение этих прямых дает решение задачи.