Задачи для самостоятельного решения. 1. Торговая фирма разработала несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей

1. Торговая фирма разработала несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели дохода представлены в таблице.

План продажи	Величина дохода

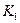
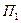
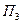
Определить оптимальный план продажи товаров.

2. Предприятие планирует выпуск трех партий новых видов товаров широкого потребления в условиях неясной рыночной конъюнктуры. Известны отдельные возможные состояния , а также возможные объемы выпуска изделий по каждому варианту, представленные в таблице.

Изделия	Объем выпуска изделий
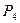
	2.2	3.8	2.8	3.2
	2.6	2.4	3.1	3.3
	3.0	2.0	1.8	2.5

Определить предпочтительный план выпуска товаров широкого потребления.

3. Пусть сторона А засылает подводную лодку в один из n районов. Сторона В, располагая m противолодочными кораблями, желает обнаружить лодку противника. Вероятность обнаружения лодки в j-м районе (j = 1,…,n) равна . Предполагается, что обнаружение подлодки каждым кораблем является независимым событием. Сторона В может посылать в различные регионы различное количество кораблей (распределение m кораблей по регионам и есть стратегия стороны В). Сторона В стремиться максимизировать вероятность обнаружения подлодки. Сторона А желает противоположного.

Вероятность обнаружения лодки в районе j, в котором находится кораблей (i – номер стратегии), равна:

,

причем 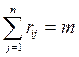. Найти оптимальное распределение противолодочных кораблей по регионам, для частного случая: m=2, n=2, /

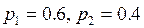1. Каждому из двух игроков выдается по бубновому и трефовому тузу. Игрок 1 получает также бубновую двойку, а игрок 2 – трефовую. При первом ходе игрок 1 выбирает и откладывает одну из своих карт, а игрок 2, не зная карты, выбранной игроком 1, также откладывает одну из своих карт. Если были отложены карты одной масти, то выигрывает игрок 1, в противном случае выигравшим считается игрок 2. Если отложены две двойки, выигрыш равен нулю. Размер выигрыша определяется картой, отложенной победителем (тузу приписывается одно очко, двойке – два). Определить оптимальную стратегию игры.

2. Фирма изготавливает железобетонные панели, используя в качестве основного сырья цемент. В связи с неопределенным спросом на изделия потребность в сырье в течение месяца также не определена. Цемент поставляется в мешках, причем известно, что потребность может составлять 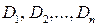мешков. Резервы сырья на складе могут составлять мешков в месяц. Учитывая, что удельные затраты на хранения сырья равны , а удельные издержки дефицитности сырья (потери, связанные с отсутствием необходимого количества цемента на складе) равны , определить оптимальную стратегию управления запасами цемента на складе для частного случая: n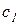=5, =5, 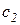=3; D= (1500, 2000, 2500, 3500, 4000), R = (1500, 2000, 2500, 3500, 4000).

3. Игрок 2 прячет некоторый ценный предмет в одном из n мест, а игрок 1 этот предмет ищет. Если он его находит, то получает сумму 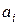, где i = 1, 2, …, n, в противном случае – не получает ничего. Определить оптимальную стратегию игры.

4. Два игрока независимо друг от друга называют по одному числу из диапазона 1 – 5. Если сумма чисел нечетная, то игрок 2 платит игроку 1 сумму, равную максимальному из чисел, если четная, то платит игрок 1. Определить оптимальную стратегию игры.

5. Два игрока имеют по n рублей и предмет ценой c>0. Каждый игрок делает заявку в запечатанном конверте, предлагая i рублей (где i одно из целых чисел от 0 до n) за предмет. Записавший большее число получает предмет и платит другому предложенную сумму. Если оба игрока заявляют одинаковую сумму, то предмет назначается без компенсирующего одностороннего платежа одного из игроков путем бросания монеты, так, что ожидаемая доля каждого в предмете составляет в этом случае половину c . Построить платежную матрицу игры и определить, имеет ли игра седловую точку.

Лабораторная работа № 7
Тема: Игры с «природой»

Цель: научиться решать прикладные экономические задачи методами теории игр с «природой» на основе критериев принятия решения и с использованием пакета прикладных программ Qmwin.