Методические указания. Постановка задачи о назначениях
Постановка задачи о назначениях
Задача характеризуется двумя множествами – ресурсов и объектов. При этом ресурсы распределяются (назначаются) по объектам. При этом один ресурс назначается на один и только один объект. Число ресурсов и объектов равны между собой и равны n. Назначение i-го ресурса на j-й объект сопряжено с затратами 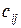
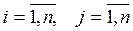 . Введем переменную
. Введем переменную 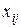 по правилу:
по правилу:
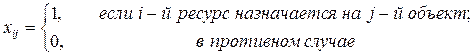
Таким образом, решение задачи может быть описано в виде матрицы 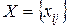 , каждая строка и каждый столбец которой содержат только одну единицу. Математическая модель задачи имеет следующий вид:
, каждая строка и каждый столбец которой содержат только одну единицу. Математическая модель задачи имеет следующий вид:
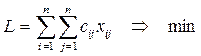
при ограничениях:
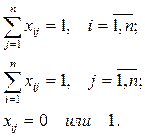
Задача о назначениях отличается, например, от транспортной задачи тем, что 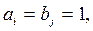 а
а 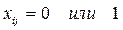 , поэтому можно было бы применить алгоритм транспортной задачи, но эффективнее работает специальный метод, называемый венгерским.
, поэтому можно было бы применить алгоритм транспортной задачи, но эффективнее работает специальный метод, называемый венгерским.
Пример. Планирование загрузки оборудования с учетом максимальной производительности станков
Постановка задачи
На предприятии четыре станка различных видов, каждый из которых может исполнять четыре различных операций по обработке деталей. Известна производительность каждого станка при выполнении каждой операции, заданная таблицей:
| Операции | Станки | ||
Определить, какую операцию, и за каким станком надо закрепить, чтобы суммарная производительность была бы максимальной при условии, что за каждым станком закреплена только одна операция.
Определим математическую постановку задачи. Целевая функция имеет вид:
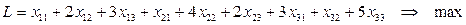
при ограничениях:
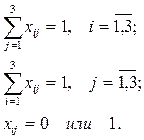
Дата добавления: 2016-04-14; просмотров: 941;
