Постановка транспортной задачи
Транспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и способов транспортирования товаров.
В общем виде задачу можно представить следующим образом. Имеется 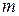 отправления:
отправления: 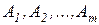 , в которых сосредоточены запасы какого-то однородного товара (груза) в количестве соответственно
, в которых сосредоточены запасы какого-то однородного товара (груза) в количестве соответственно 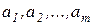 единиц. Кроме того, имеется
единиц. Кроме того, имеется 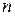 пунктов назначения:
пунктов назначения: 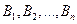 , подавших заявки соответственно
, подавших заявки соответственно 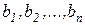 единиц товара. Стоимость перевозки единицы груза из пункта
единиц товара. Стоимость перевозки единицы груза из пункта 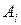 в пункт
в пункт 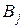 равна
равна 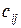 . Требуется составить план перевозок, позволяющий обеспечить все заявки и имеющий минимальную стоимость.
. Требуется составить план перевозок, позволяющий обеспечить все заявки и имеющий минимальную стоимость.
Транспортные задачи могут быть закрытыми, когда суммарные запасы равны суммарным потребностям:
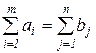 , (1)
, (1)
и открытыми, в противоположном случае:
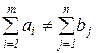 . (2)
. (2)
Обозначим через 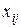 количество груза перевозимого из пункта
количество груза перевозимого из пункта 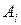 в пункт
в пункт 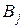 . Тогда математическая модель закрытой транспортной задачи имеет вид:
. Тогда математическая модель закрытой транспортной задачи имеет вид:
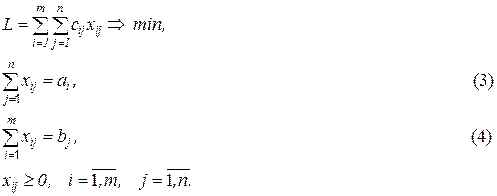
Особенностью этой модели является то, что все коэффициенты при переменных в уравнениях (3) и (4) равны единице. Кроме того, не все уравнения из (3) и (4) линейно независимы, т.к. при сложении всех этих уравнений должно выполниться (1). Все это позволяет использовать при решении транспортных задач более простые методы, нежели симплекс-метод, в частности, метод потенциалов.
Пример. Определение эффективного варианта доставки изделий к потребителю
Постановка задачи
На складах 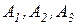 имеются запасы продукции в количествах 90, 400, 110 т. соответственно. Потребители
имеются запасы продукции в количествах 90, 400, 110 т. соответственно. Потребители 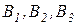 должны получить эту продукцию в количествах 140, 300, 160 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы таблицей (усл. ед.):
должны получить эту продукцию в количествах 140, 300, 160 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы таблицей (усл. ед.):
| 
| 
| |
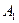
| |||
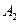
| |||
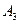
|
Обозначим через 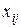 количество продукции, перевозимой со склада
количество продукции, перевозимой со склада 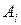 потребителю
потребителю 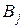 . Тогда целевая функция имеет вид:
. Тогда целевая функция имеет вид:
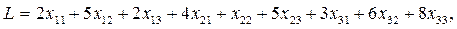
при ограничениях:
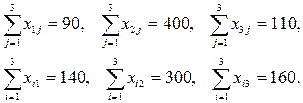
Дата добавления: 2016-04-14; просмотров: 777;
