Расстояние между скрещивающимися прямыми определяется длиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые.
Для того чтобы через скрещивающиеся прямые m и f провести взаимно параллельные плоскости a и b, достаточно через точку 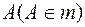 провести прямую р, параллельную прямой f, а через точку
провести прямую р, параллельную прямой f, а через точку 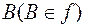 — прямую k, параллельную прямой т. Пересекающиеся прямые m и p, f и k определяют взаимно параллельные плоскости a и b.Расстояние между плоскостями a и b равно искомому расстоянию между скрещивающимися прямыми m и f.
— прямую k, параллельную прямой т. Пересекающиеся прямые m и p, f и k определяют взаимно параллельные плоскости a и b.Расстояние между плоскостями a и b равно искомому расстоянию между скрещивающимися прямыми m и f.
Можно предложить и другой путь для определения расстояния между скрещивающимися прямыми, который состоит в том, что с помощью какого-либо способа преобразования ортогональных проекций одна из скрещивающихся прямых переводится в проецирующее положение. В этом случае одна из проекций прямой вырождается в точку. Расстояние между новыми проекциями скрещивающихся прямых (точкой 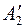 и отрезком
и отрезком 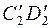 ) является искомым.
) является искомым.
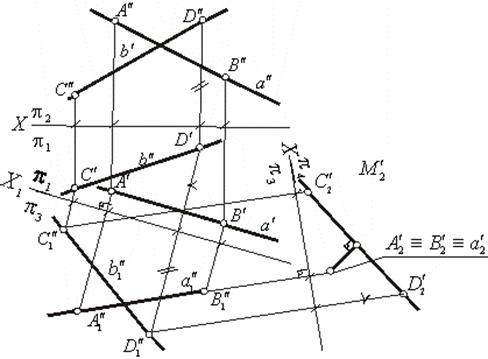
На рис. 1 приведено решение задачи на определение расстояния между скрещивающимися прямыми а и b, заданными отрезками [АВ] и [CD]. Решение выполняют в следующей последовательности:
1.Переводят одну из скрещивающихся прямых (а) в положение,
параллельное плоскости 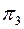 ; для этого переходят от системы плоскостей проекции
; для этого переходят от системы плоскостей проекции 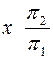 к новой
к новой 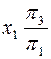 , ось x1 проводят параллельно горизонтальной проекции прямой а . Определяют
, ось x1 проводят параллельно горизонтальной проекции прямой а . Определяют 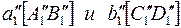 .
.
2. Путем замены плоскости 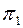 плоскостью
плоскостью 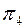 переводят прямую a в положение
переводят прямую a в положение 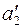 , перпендикулярное плоскости
, перпендикулярное плоскости 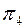 (новую ось x2 проводят перпендикулярно
(новую ось x2 проводят перпендикулярно 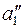 ).
).
3. Строят новую горизонтальную проекцию прямой 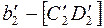 .
.
 |
4. Расстояние от точки
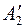 до прямой
до прямой 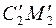 (отрезок
(отрезок 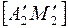 ) является искомым.
) является искомым.
Рис.1- Определение расстояния между скрещивающимися прямыми
Следует иметь в виду, что переведя прямую a в положение, перпендикулярное плоскости 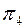 ,мы обеспечиваем перпендикулярность любой плоскости, содержащей прямую a, плоскости
,мы обеспечиваем перпендикулярность любой плоскости, содержащей прямую a, плоскости 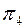 , в том числе и плоскости a, определяемой прямыми a и m
, в том числе и плоскости a, определяемой прямыми a и m 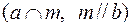 . Если мы теперь проведем прямую n, параллельную а и пересекающую прямую b, то мы получим плоскость b, являющуюся второй плоскостью параллелизма, в которую заключены скрещивающиеся прямые а и b. Так как
. Если мы теперь проведем прямую n, параллельную а и пересекающую прямую b, то мы получим плоскость b, являющуюся второй плоскостью параллелизма, в которую заключены скрещивающиеся прямые а и b. Так как 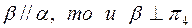 .
.
Более подробные сведения приведены в методических указаниях [5].
Образец решения задачи по определению кратчайшего расстояния между скрещивающимися прямыми AS и BC по приведенному алгоритмуприведен на рис. Б1. Полученный отрезок MN с плоскости 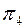 последовательно возвращаем на все плоскости проекций, т.е. плоскости
последовательно возвращаем на все плоскости проекций, т.е. плоскости 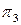 ,
, 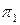 ,
, 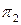 .
.
Дата добавления: 2016-04-14; просмотров: 941;
