Решение первой задачи (определение истинной величины

основания пирамиды ABC)

Решение первой задачи, определение истинной величины основания пирамиды ABC рекомендуется решать методом вращения вокруг горизонтали или фронтали (приложение Б, рис. Б1).

Порядок выполнения работы следующий.

Выбрав в плоскости фигуры АВС некоторую линию уровня (например, горизонталь h) и приняв ее за ось вращения, поворачиваем плоскость фигуры так, чтобы она стала параллельна плоскости 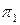. После этого фигура проектируется на 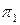в натуральную величину. В процессе вращения каждую из точек А и В (точка С остается на месте, так как лежит на горизонтали) перемещаются в горизонтально-проецирующих плоскостях, перпендикулярных оси вращения. Натуральную величину радиуса вращения находят методом прямоугольного треугольника. Стороны полученной натуральной величины фигуры АВС обвести красной пастой. Все вспомогательные построения необходимо сохранить на чертеже и показать их тонкими сплошными линиями синей (зеленой) пастой. Более подробные сведения приведены в методических указаниях [5].

3.2. Решение второй задачи (определение расстояния от вершины S до плоскости основания ABC)

Решение второй задачи, определениерасстояния от вершины S до плоскости основания ABC, рекомендуется решать методом плоско параллельного переноса (приложение Б, рис. Б1).

Соблюдая правила вращения геометрических фигур вокруг оси, перпендикулярной плоскости проекций, необходимо выполнить два действия:

1- привести плоскость АВС в положение проецирующей плоскости,

т .е. перпендикулярной плоскости проекции 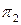. Для получения фронтально-проецирующей плоскости необходимо горизонталь 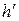(линия 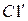) вместе с системой всех точек плоскости (треугольника АВС) поставить в положение, перпендикулярное фронтальной плоскости проекций .

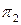Используем метод плоско - параллельного переноса. Линия перемещения точки на фронтальной плоскости осуществляется по прямой, параллельной оси проекций.

2- определить расстояние от точки S до заданной плоскости. Оно равно отрезку перпендикуляра 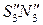опущенного из точки S на плоскость α, Выродившуюся на новой фронтально-проецирующей плоскости проекций в прямую линию. Получив основание перпендикуляра 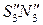, строим его горизонтальную проекцию на исходном чертеже, согласно теореме прямого угла, получаем отрезок 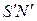. Проекции полученной натуральной величины перпендикуляра обвести красной пастой.

Более подробные сведения приведены в методических указаниях [5].

3.3. Решение третьей задачи (определение расстояния между скрещивающимися прямыми AS и BC)

Решение третьей задачи, определение расстояния между скрещивающимися прямыми, рекомендуется решать методам замены плоскости проекций (приложение Б, рис. Б1).