Решение четвертой задачи (определение величины

двугранного угла при ребре АВ)

Решение четвертой задачи, определениевеличины двугранного угла при ребре АВ рекомендуется решать двумя методами: методом замены плоскости проекций и вращением вокруг оси перпендикулярной плоскости проекции (приложение Б, рис. Б1).

Двугранный угол измеряется линейным углом, составленным линиями пересечения граней двугранного угла с плоскостью, перпендикулярной к его ребру. Для того чтобы линейный угол проецировался на плоскость проекций в натуральную величину, надо новую плоскость проекций поставить перпендикулярно к ребру двугранного угла.

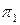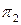При применении способа замены плоскостей нужно иметь в виду, что фигура не меняет своего положения в пространстве, плоскость же проекций и заменяют новой плоскостью, соответственно 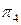или 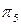. При построении проекций фигуры на новой плоскости проекций необходимо помнить, что происходит переход от одного изображения к другому, на котором соответственные проекции точек также расположены на линиях связи. Координаты точки на новой плоскости проекций равна координате точки на заменяемой плоскости проекций.

Первую часть задачи по приведению линии AB в положение параллельное плоскости 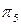осуществляем методом замены плоскости проекций. Вторую часть задачи по приведению линии AB в положение перпендикулярное плоскости 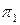проводим методом вращения вокруг оси перпендикулярной плоскости проекции 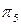в точке 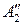. При этом на плоскости 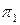линия AB проецируется в точку, а две грани пирамиды в линию, угол между этими линиями и будет искомым. Выполнив все построения в карандаше, чертеж обводят цветной пастой. Конечное построение двугранного угла выполнить красным цветом. Более подробные сведения приведены в методических указаниях [5].

Контрольные вопросы при защите РГР 2

1 В чем заключается способ вращения?

2 Назвать элементы вращения.

3 Как перемещаются проекции точки относительно плоскостей проекций при вращении ее вокруг горизонтально-проецирующей оси?

4 Какая из проекций отрезка прямой или плоской фигуры не изменяет своей величины (формы) при вращении вокруг фронтально-проецирующей оси?

5 Как прямую общего положения повернуть до положения проецирующей прямой?

6 Какую проецирующую прямую следует принять за ось вращения, чтобы плоскость общего положения стала в результате вращения фронтально-проецирующей?

7 В чем состоит сущность способа плоскопараллельного перемещения?

8 В какой проецирующей плоскости перемещается точка при вращении вокруг горизонтали? Фронтали?

9 Как определить радиус вращения точки при ее вращении вокруг горизонтали? Фронтали ?

10 Что является осью вращения при совмещении заданной плоскости с горизонтальной (фронтальной) плоскостью проекции?

11 В чем состоит способ замены плоскостей проекций?

12 Какие координаты точек остаются неизменными при замене горизонтальной (фронтальной) плоскости проекций?

13 Как надо располагать новые плоскости проекций, чтобы отрезок прямой общего назначения проецировался в натуральную величину? В точку?

14 Как расположить новую плоскость проекций, чтобы заданная плоскость стала проецирующей?

15 При каком расположении треугольника можно определить натуральную величину с помощью замены только одной плоскости проекций?

16 В каком случае двугранный угол между плоскостями проецируется на плоскость проекций в натуральную величину?

17 В чем состоит сущность способа вращения вокруг оси перпендикулярной плоскости проекции?