Метод концентрических сфер
Задача. Построить линию пересечения двух поверхностей вращения: конуса (Ф1) и цилиндра (Ф2). Графическое оформление задачи приведено на рис. 8.
Метод концентрических сфер применяется при одновременном выполнении трех условий:
1) пересекающиеся поверхности должны быть поверхностями вращения;
2) оси поверхностей должны пересекаться;
3) поверхности должны иметь общую плоскость симметрии, параллельную одной из плоскостей проекций.
Анализ и решение задачи:
 |
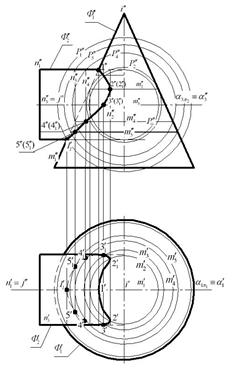Рис.8
Первый шаг алгоритма записываем аналогично методу плоских посредников:
1) 
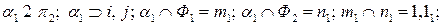
где точка 1 – верхняя, точка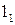 
- нижняя.
Для нахождения остальных точек, принадлежащих искомой линии, вводим сферические посредники. Сферические посредники должны проводиться из точки пересечения осей поверхностей, поскольку только в этом случае они (посредники) окажутся соосными с каждой из пересекающихся поверхностей. В качестве минимального посредника должна приниматься большая из сфер - Р2, вписанных из точки пересечения осей (i и ј) в каждую поверхность в отдельности. Это связано с тем, что меньшая из вписанных сфер - Р0 не дает линии пересечения (или касания) с другой поверхностью (Φ1) и, следовательно, не дает точки, общей для пересекающихся поверхностей. В качестве максимального посредника принимается сфера (Р1), радиус которой равен расстоянию от точки пересечения осей i и ј до наиболее удаленной точки ( 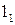) пересечения очерков поверхностей Φ1 и Φ2. Остальные сферические посредники должны быть больше минимального и меньше максимального. Для определения минимального посредника Р на фронтальной плоскости проекций проводим сферы Р0 и Р2 (проекции 
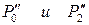), вписанные соответственно в поверхности Φ2 и Φ1 (проекции 
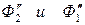). В качестве минимального посредника принимаем сферу Р2 (проекция 
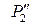), отвергая Р0 (проекция 
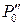). Через точки касания сферы Р2 (проекция 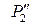) с конусом Φ1 (проекция 
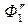) проводим линию m2 (проекции 
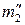) касания (напомним, что касание – есть частный случай пересечения) ее с конусом Φ1 (проекции 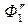), а через точки пересечения Р2 (проекция 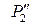) с цилиндром Φ2 (проекции 
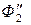) – линию n2 (проекция 
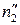) пересечения посредника Р2 с цилиндром Φ2. Находим точки 
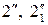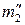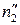пересечения линий в пространстве – (окружностей) и . Строим горизонтальную проекцию 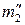параллели m2, и по линии связи сносим на нее точки 
.
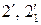Записываем второй шаг алгоритма: 2) Р2 > Р0; Р2 ∩ Φ1 = m2; Р2 ∩ Φ2 = n2; m2 ∩ n2 =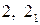 
- левые точки. В качестве максимального посредника принимаем сферу Р1 (проекция 
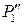), проходящую через ранее полученную точку 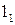(проекция 
).
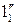Остальные сферические посредники должны быть радиусом больше принятого минимального посредника Р2 и меньше максимального посредника Р1.
Для определения границы зоны видимости горизонтальной проекции искомой линии ℓ через условный экватор цилиндра Φ2 (через ось j) проводим горизонтальную плоскость уровня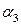 
(след-проекция 
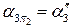). Эта плоскость 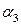пересекает конус Φ1 по окружности m3 (проекция 
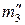), а цилиндр Φ2 по прямоугольнику, фронтальная проекция которого есть прямая 
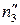, а горизонтальная проекция 
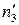совпадает с горизонтальным очерком 
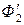цилиндра Φ2. Горизонтальные проекци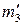и 
и 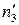, пересекаясь, дают точки 3 и 
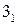(проекци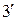и 
и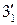 
). Фронтальные проекци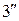и 
и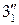 
этих точек находятся на следе-проекции 
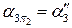плоскости 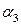по линиям проекционной связи.
Записываем третий шаг алгоритма:
3) 
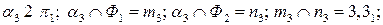- точки, определяющие границы видимости для горизонтальной плоскости проекций, одновременно являющиеся ближней и дальней точками.
Все найденные точки являются опорными. Далее следует перейти к построению произвольных точек. Проводим сферический посредник Р4, больший P2 и меньший Р1 (проекция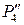 
). Находим фронтальные проекци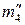и 
и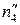 
линий m4 и n4 пересечения посредника Р4 с поверхностями конуса и цилиндра и точки 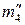и 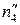, пересечения этих линий. Строим горизонтальную проекцию 
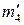параллели m4 и на ней по линии связи – горизонтальные проекции 
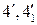искомых точек. Записываем четвертый шаг алгоритма: 4) Р1 > Р4 > Р2; Р4 ∩ Φ1 = m4; Р4 ∩ Р2 = n4; m4 ∩ n4 = 4, 
.
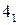Аналогично решается и записывается пятый шаг алгоритма: 5) Р1 > Р5 > Р2; Р5 ∩ Φ1 = m5; Р5 ∩ Φ2 = n5; m5 ∩ n5 = 5,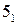 
.
И заключительный шаг алгоритма: ℓ =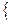 
.
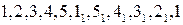
Образец выполнения эпюра 4 приведен в приложение Г.
Дата добавления: 2016-04-14; просмотров: 1437;