Методические указания. Данные для выполнения эпюра брать из соответствующих рисунков приложения Г (рис.Г1-Г3, табл Г1) , номер варианта соответствует порядковому номеру в учебном
Данные для выполнения эпюра брать из соответствующих рисунков приложения Г (рис.Г1-Г3, табл Г1) , номер варианта соответствует порядковому номеру в учебном журнале. Образец выполнения работы приведен в приложение Г( рис. Г4). В левой половине листа намечают изображение трех поверхностей вращения согласно своему варианту. Выбирают для двух пересекающихся поверхностей способ вспомогательных секущих плоскостей, а для двух других пересекающихся поверхностей способ концентрических сфер. Можно чертеж разбить, т.е. сделать отдельно два чертежа, один для метода секущих плоскостей, другой для метода концентрических окружностей (как показано на рис. Г4).
На эпюре рекомендуется вычерчивать только элементы, необходимые для решения поставленной задачи. Допускается решение задач выполнять без проведения осей проекций.
Выполнение задания начинается с прочтения чертежа: выясняется из каких геометрических тел состоит поверхность детали (объекта). Стараются представить модель пересекающихся тел, например как на (рис. 6).
Исходя из общих правил, которые обуславливают выбор метода решения, выбираем для первой модели метод секущих плоскостей, для второй модели, метод концентрических окружностей.
В качестве примеров на построение линии пересечения напомним метод вспомогательных секущих плоскостей (рис. 7) и метод вспомогательных концентрических сфер (рис.8). На рис. 7 показано построение проекции линии пересечения поверхности прямого кругового конуса и сферы.
 |
Рисунок 6 - Модели пересекающихся тел
Прежде чем приступить к выполнению задания, студенту необходимо определить, каким из рассматриваемых ниже методов следует решить задачу по заданному варианту.
Задачу нужно решить одним из двух методов: методом плоских посредников или методом концентрических сфер.
В первом случае в качестве вспомогательного посредника выбираются плоскости частного положения. Во втором случае - концентрические сферы.
Посредники должны в любом случае располагаться (пересекать обе поверхности) таким образом, чтобы линии их пересечения с каждой поверхностью являлись наипростейшими, т.е. окружностями или прямыми.
Построение следует начинать с определения опорных точек – точек, расположенных на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой); точек, удаленных на максимальное и минимальное расстояния от плоскостей проекций (верхней, нижней, левой, правой, ближней, дальней и т.д.). Если опорных точек окажется недостаточно для определения искомой линии пересечения, необходимо найти несколько произвольных точек. Общий алгоритм решения задачи, независимо от выбранного метода заключается в следующем:
1) пересечь заданные поверхности (Φ1 и Φ2) вспомогательным геометрическим элементом – посредником (α1);
2) построить линии (m1 и n1) пересечения посредника (α1) с каждой поверхностью в отдельности.
3) найти точки (1 и 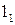 ) пересечения полученных линий (m1 и n1);
) пересечения полученных линий (m1 и n1);
4) повторить этот алгоритм необходимое количество раз;
5) соединить между собой полученные точки (1, 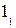 , 2,
, 2, 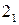 и т.д.) в надлежащей последовательности, чтобы получить искомую линию пересечения (ℓ) двух поверхностей (Φ1 и Φ2). Символическая запись алгоритма выглядит следующим образом:
и т.д.) в надлежащей последовательности, чтобы получить искомую линию пересечения (ℓ) двух поверхностей (Φ1 и Φ2). Символическая запись алгоритма выглядит следующим образом:
1) α1 ∩ Φ1 = m1; α1 ∩ Φ2 = n1; m1 ∩ n1 = 1, 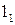 - первый шаг;
- первый шаг;
2) α2 ∩ Φ1 = m2; α2 ∩ Φ2 = n2; m2 ∩ n2 = 2, 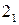 - второй шаг;
- второй шаг;
и т. д.
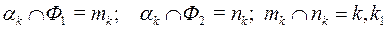 - последний шаг,
- последний шаг,
где 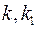 - промежуточные точки.
- промежуточные точки.
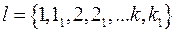
Дата добавления: 2016-04-14; просмотров: 776;
