Метод плоских посредников
Задача: Построить линию пересечения двух поверхностей вращения: конуса (Φ1) и сферы (Φ2). Графическое оформление задачи приведено на рис. 7.
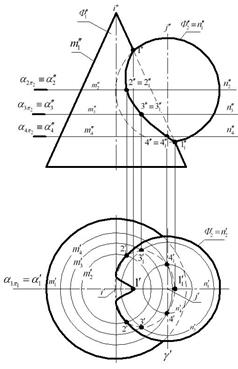 |
Рис. 7
Символическая запись условия задачи: Φ1, Φ2; Φ1 ∩ Φ2 = ℓ ?
Анализ и решение задачи:
1) пересекаются две поверхности вращения второго порядка, следовательно, линия пересечения ℓ является кривой четвертого порядка.
2) так как вид пересечения – «врезка» (несквозное пересечение), то получается одна линия пересечения ℓ.
3) поверхности имеют общую плоскость симметрии α1, параллельную фронтальной плоскости проекций, значит пересечение их фронтальных очерков 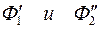 дает пару характерных точек
дает пару характерных точек  – верхнюю и
– верхнюю и  - нижнюю.
- нижнюю.
4) в качестве посредников для последующих построений в этой задаче целесообразно принимать горизонтальные плоскости α2, α3 и т. д., поскольку линии пересечения ими каждой из поверхностей являются наипростейшими (окружностями).
5) границей зоны видимости искомой кривой ℓ для горизонтальной плоскости проекций является экватор сферы, поэтому плоскость – посредник α2 проведенная через экватор сферы Φ2, дает на втором шаге алгоритма принадлежащие экватору точки 2 и 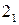 , являющиеся границами зоны видимости для горизонтальной плоскости проекций. Эти же точки являются самыми левыми.
, являющиеся границами зоны видимости для горизонтальной плоскости проекций. Эти же точки являются самыми левыми.
6) границами видимости для фронтальной плоскости проекций являются главные фронтальные меридианы и принадлежащие им точки 1 и 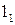 .
.
Таким образом, построение линии пересечения поверхностей сводится к следующему.
Во-первых, проводим плоскость α1, параллельную фронтальной плоскости проекций через оси i и ј поверхностей. На горизонтальной плоскости проекций – это след-проекция 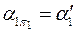 , параллельная оси х. На фронтальной проекции находим точки
, параллельная оси х. На фронтальной проекции находим точки 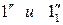 пересечения очерков
пересечения очерков 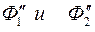 . Сносим полученные точки на горизонтальный след-проекцию
. Сносим полученные точки на горизонтальный след-проекцию 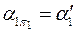 плоскости α1 с учетом видимости (точка
плоскости α1 с учетом видимости (точка 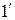 ' – видимая,
' – видимая, 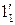 – невидимая). Записываем первый шаг алгоритма в виде:
– невидимая). Записываем первый шаг алгоритма в виде:
1) 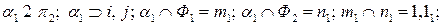
где точка 1 – верхняя, точка 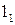 - нижняя.
- нижняя.
Отметим, что алгоритм записывается для пространства, а построение проекций точек и линии ℓ производится для каждой плоскости проекций с обязательным обозначением всех элементов построения.
Во-вторых, через экватор сферы Φ2 проводим плоскость-посредник α2, параллельную горизонтальной плоскости проекций (см. 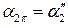 ). Параллели m2 и n2 фронтальной проекции неразличимы, так как их проекции m2" и n2" частично накладываются друг на друга. Поэтому строим их горизонтальные проекции m2' и n2', как окружности соответствующих радиусов и точки
). Параллели m2 и n2 фронтальной проекции неразличимы, так как их проекции m2" и n2" частично накладываются друг на друга. Поэтому строим их горизонтальные проекции m2' и n2', как окружности соответствующих радиусов и точки 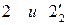 их пересечения. Фронтальные проекции
их пересечения. Фронтальные проекции 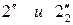 " этих точек находим на след-проекции
" этих точек находим на след-проекции 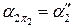 плоскости α2 по линиям проекционной связи. Записываем второй шаг алгоритма:
плоскости α2 по линиям проекционной связи. Записываем второй шаг алгоритма:
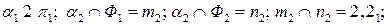
2) 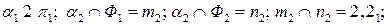
точка 2 – левая ближняя, точка 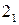 - левая дальняя. Обе точки – границы видимости.
- левая дальняя. Обе точки – границы видимости.
В-третьих, произвольно проводим плоскость α3, параллельную плоскости 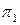 . Аналогично второму шагу, находим горизонтальные проекции
. Аналогично второму шагу, находим горизонтальные проекции 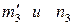 линий пересечения этой плоскости с каждой поверхностью и горизонтальные проекции
линий пересечения этой плоскости с каждой поверхностью и горизонтальные проекции 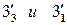 точек
точек 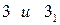 , а затем на следе-проекции
, а затем на следе-проекции 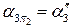 – фронтальные проекции
– фронтальные проекции 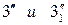 этих точек. Записываем третий шаг алгоритма:
этих точек. Записываем третий шаг алгоритма:
3) 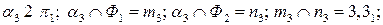 - произвольные точки. Аналогично можно было бы получить точки под номерами 4, 5 и т. д., но для данной задачи в этом нет необходимости, так как характер и форма кривой определены достаточно полно.
- произвольные точки. Аналогично можно было бы получить точки под номерами 4, 5 и т. д., но для данной задачи в этом нет необходимости, так как характер и форма кривой определены достаточно полно.
В-четвертых, соединяем полученные точки между собой. Поскольку искомая кривая ℓ является замкнутой, ее построение можно начинать с любой точки и в любом направлении, например 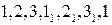 .
.
Заключительный этап алгоритма может быть записан в виде:
ℓ = 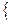
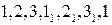
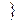 или ℓ =
или ℓ = 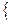
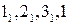
 .
.
Дата добавления: 2016-04-14; просмотров: 1850;
