Модель поставок со скидкой
Рассмотрим ситуацию, описываемую в целом основной моделью, но с одной особенностью, которая состоит в том, что товар можно поставлять по льготной цене (со скидкой), если размер партии достаточно велик. Иными словами, если размер партии qне менее заданного числа q 0, товар поставляется по цене с0, где с0 < с.
Функция общих издержек C ( q )задается в таком случае следующим образом:
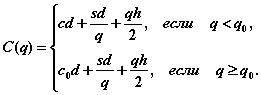
Нетрудно видеть, что функция C ( q )в точке q=q 0 разрывна.
Обе функции
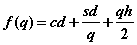
и
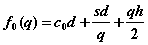
имеют минимум в точке, где
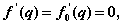
т.е. в точке
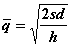 .
.
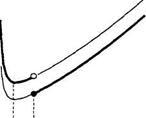
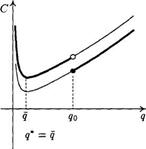
 Для выяснения вопроса о том, какой размер партии оптимален, следует сравнить значения функции C ( q )в точках qи q 0,и та точка, где функция C ( q )принимает меньшее значение, будет оптимальным размером партии q *в модели поставок со скидкой (см. рис. 8.9, 8.10).
Для выяснения вопроса о том, какой размер партии оптимален, следует сравнить значения функции C ( q )в точках qи q 0,и та точка, где функция C ( q )принимает меньшее значение, будет оптимальным размером партии q *в модели поставок со скидкой (см. рис. 8.9, 8.10).
Замечание. Может случиться так, что C ( 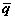 )= C ( q 0 ). Тогда, разумеется, q* =
)= C ( q 0 ). Тогда, разумеется, q* = 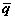 = q 0.
= q 0.
Пример 3 Предположим, что интенсивность равномерного спроса составляет 1000 единиц товара в год. Организационные издержки равны 10 УЕ, издержки на хранение — 4 УЕ. Цена единицы товара равна 5 УЕ, однако если размер партии не менее 500 единиц, цена снижается до 4 УЕ. Найти оптимальный размер партии.
Решение. Здесь
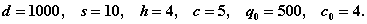
Общие издержки определяются функцией C ( q ):
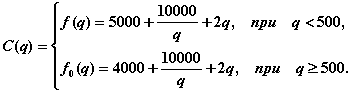
Найдем точку локального минимума. Имеем:
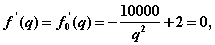
откуда
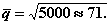
Поскольку 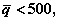 то
то 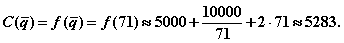
В точке 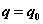 получаем
получаем
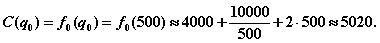
Таким образом, 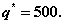
Дата добавления: 2016-04-14; просмотров: 1410;
