Управление запасами

Вопросы управления закупками и поставками взаимоувязаны с вопросами управления запасами ресурсов. После решения вопросов, что нужно купить, следует решить – сколько нужно приобрести, т.е. определяется, какой объем каждого ресурса необходимо иметь в виде определенного запаса с целью:

• минимизации риска приостановки производственного процесса в связи с нехваткой ресурса для производства работ;
• обеспечения ритмичного производства между моментами поставок ресурса.

Задача определения регламента и объемов поставок и запасов относится к классу оптимизационных задач управления ресурсами. В качестве целевой функции в управлении запасами выступают суммарные затраты на содержание запасов, на складские операции, потери от порчи при хранении и пр.

Под управлением запасами понимается контроль за состоянием запасов и принятие решений, нацеленных на экономию времени и средств за счет минимизации затрат по содержанию необходимых запасов, необходимых для эффективной реализации проекта.

Управление запасами осложняется постоянно меняющейся обстановкой, в которой осуществляется планирование закупок, поставок и формирование запасов ресурсов. Цель системы управления запасами – бесперебойное обеспечение процессов выполнения работ по проекту в установленные сроки и с запланированным качеством при минимально возможных затратах на содержание запасов.

Целесообразное и эффективное управление запасами позволяет:

• уменьшить производственные потери из-за дефицита материалов;
• свести к минимуму излишки запасов ресурсов, которые по сути замораживают денежные средства;
• снизить риск перебоев в запланированном ходе работ по проекту;
• снизить затраты на хранение товарно-материальных запасов.

Система управления запасами решает следующие основные задачи:

• контроль и учет уровня запасов;
• определение размера резервного запаса для каждого ресурса, зависящего от необходимости непрерывного обеспечения работ проекта;
• расчет оптимального размера заказа ресурса;
• определение интервала времени между заказами.

Контроль уровня запасов ведется по всем группам ресурсов и состоит в учете наличия ресурсов и отслеживания момента, когда следует осуществить заказ очередной партии ресурсов.

Одним из наиболее известных методов контроля уровня запасов является АВС-метод – способ учета и контроля за состоянием запасов заключающийся в разбиении номенклатуры ресурсов на три подмножества – А, В и С. Метод АВС-контроля товарно-материальных запасов базируется на разделении запасов сырья и материалов на три категории по степени важности отдельных видов ресурсов в зависимости от их удельной стоимости.

К категории А относится ограниченное количество наиболее ценных видов ресурсов, которые требуют постоянного подробного учета и контроля (возможно, ежедневного). Для этих ресурсов обязателен расчет оптимального размера заказа.

К категории В относятся те виды товарно-материальных запасов, которые в меньшей степени важны для проекта и которые оцениваются и проверяются при ежемесячной инвентаризации. Для этой категории ресурсов, как и для категории А, приемлемы методики определения оптимального размера заказа.

К категории С относится широкий ассортимент оставшихся малоценных видов ресурсов, закупаемых обычно в большом количестве.

Из АВС-метода вытекает, в частности, правило 20/80. Установлено, что в большинстве случаев 75% стоимости запасов охватывает около 10 % наименований номенклатуры ресурсов (подмножество А), 20 % стоимости – соответственно 25% наименований (подмножество В), 5 % стоимости – 65 % наименований (подмножество С). Во многих случаях оказывается, что 20 % наиболее потребляемых ресурсов составляют около 80 % стоимости запасов.

Наиболее распространенным инструментом в управлении запасами, направленным на минимизацию суммарных затрат, традиционно признается модель оптимального размера заказа.

Основная модель

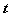Важнейшую роль в наших рассуждениях будет играть функция изменения запаса. Это связь между количеством единиц товара на складе (обозначим его через ) и временем . Будем считать, что имеется один вид товара.

Если на товар имеется спрос, то функция изменения запаса 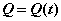убывает. Если товар, наоборот, завозят на склад, то эта функция возрастает. Будем считать возможным мгновенное пополнение запаса.

Затраты, связанные с запасами, можно разделить на три части.

А Стоимость товара.

Б Организационные издержки. Это расходы, связанные с оформлением товара, его доставкой, разгрузкой и т.д.

В Издержки на хранение товара. Это затраты на аренду склада, амортизацию в процессе хранения и т.д.

Рассмотрим основные величины и предположения относительно них, принятые в рамках основной модели. Мы будем в основном использовать в качестве единицы измерения денежных средств условные единицы (УЕ), это могут быть гривны, доллары и т.д.; в качестве единицы измерения времени – год, хотя можно было бы взять месяц, квартал и т.п.

1. Цена единицы товара – с УЕ. Цена постоянна, рассматривается один вид товара.
2. Интенсивность спроса – d единиц товара в год. Будем считать, что спрос постоянный и непрерывный.
3. Организационные издержки – s УЕ за одну партию товара. Будем считать, что организационные издержки не зависят от размера поставки, т.е. от количества единиц товара в одной партии.
4. Издержки на хранение запаса – h УЕ на единицу товара в год. Будем считать эти издержки постоянными.
5. Размер одной партии товара постоянен – q единиц. Партия поступает мгновенно в тот момент, когда возникает дефицит, т.е. когда запас на складе становится равным нулю.

При сделанных предположениях график функции изменения запаса будет таким, как показано на рис.8.6: он состоит из повторяющихся циклов пополнения запаса между двумя соседними дефицитами. Вертикальные отрезки отвечают мгновенному пополнению запаса.

Параметры с, d, s, h считаются заданными. Задача управления запасами состоит в выборе параметра q таким образом, чтобы минимизировать годовые затраты.

Для решения сформулированной задачи надо прежде всего выразить эти затраты через параметры с, d, s, h, q.

А Поскольку годовая интенсивность спроса равнаd, а цена единицы товара – с, то общая стоимость товара в год равна с d.

Б Поскольку в одной партии qединиц товара, а годовой спрос равен d, то число поставок равно d / q. В течение года организацион­ные издержки равны .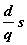

Рисунок 8.6

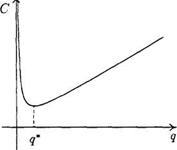
Рисунок 8.7

В Средний уровень запаса равен отношению площади под гра­фиком за цикл к продолжительности цикла. Этот средний уровень равен q /2(на рис. 8.6 обозначен пунктиром). Поскольку годовые из­держки на хранение единицы товара равны h, то общие издержки на хранение составляют .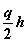

Таким образом, общие издержки Свычисляются по формуле

.

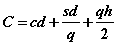Еще раз напомним, что в рамках модели параметры с, d , s , hсчи­таются заданными и требуется найти такое число q *, чтобы функция С =C ( q )принимала наименьшее значение на множестве q> 0 имен­но в точке q *.

График функции С = C ( q )показан на рис. 8.7.

Для нахождения точки q *минимума функции С = C ( q )найдем ее производную (с, d , s , h— фиксированные числа):

.

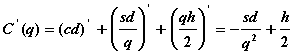Приравнивая 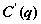к нулю, получаем

.

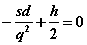Отсюда можно найти 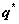. Имеем:

.

Пример 1 Пусть интенсивность равномерного спроса составляет 1000 единиц товара в год. Организационные издержки равны 10 УЕ, издержки на хранение – 4 УЕ на единицу товара в год, цена товара – 5 УЕ.

Определить оптимальный размер партии в предположении, что система подчиняется основной модели.

Решение. Имеем:

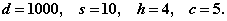
Общие затраты равны:

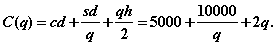
Тогда

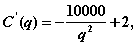
а оптимальный размер поставки 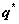является решением уравнения 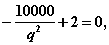т.е.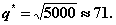

Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год 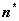и соответствующую продолжительность цикла изменения запаса :

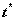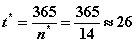дней.

Модель производственных поставок

В основной модели предполагалось, что поступление товаров на склад происходит мгновенно. Это предположение достаточно хоро­шо отражает ситуацию, когда товар поставляется в течение одного дня (или ночи). Если товары поставляются с работающей производ­ственной линии, необходимо модифицировать основную модель. В этом случае к параметрам с, d, sи hдобавляется еще один — про­изводительность производственной линии р (единиц товара в год). Будем считать ее заданной и постоянной.

Эта новая модель называется моделью производственных поста­вок. Величина q по-прежнему обозначает размер партии. В начале каждого цикла происходит "подключение" к производственной ли­нии, которое продолжается до накопления q единиц товара. После этого пополнение запасов не происходит до тех пор, пока не возник дефицит.

График функции изменения запаса имеет вид, изображенный на рис. 8.8.

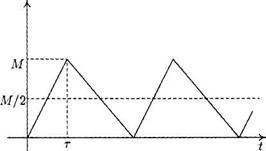
Рисунок 8.8

Общие издержки C ( q ), как и в основной модели, состоят из трех частей.

AОбщая стоимость товара в год равна cd.

БГодовые организационные издержки равны .

В Издержки на хранение вычисляются следующим образом. Пусть 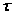— время поставки (рис. 8.8). В течение этого времени проис­ходит как пополнение (с интенсивностью р), так и расходование (с интенсивностью d)запаса. Увеличение запаса происходит со скоро­стью p — d. Поэтому достигнутый к концу периода пополнения запаса максимальный его уровень Мвычисляется по формуле

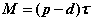(заметим, что М < q).

Однако,

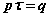
(за время 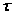при интенсивности производства рпроизведено qединиц товара). Из последних двух равенств следует, что

.

Средний уровень запаса, как и в основной модели, равен полови­не максимального, т. е. М/2. Таким образом, издержки на хранение запаса равны

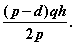
Общие издержки вычисляются по формуле

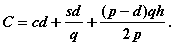
Оптимальный размер поставок q *получаем из уравнения

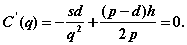
Имеем:

Пример 2 Интенсивность равномерного спроса составляет 1 тыс. единиц товара в год. Товар поставляется с конвейера, произ­водительность которого составляет 5 тыс. единиц в год. Организаци­онные издержки равны 10 УЕ, издержки на хранение — 2 УЕ, цена единицы товара — 5 УЕ. Чему равен оптимальный размер партии?

Решение. Имеем:

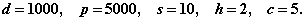
Далее,

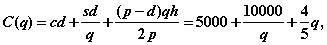
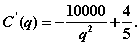
В итоге получаем

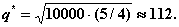
Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год 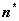и соответствующую продолжительность поставки и продолжительность цикла пополнения запаса :

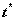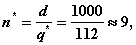
дней,

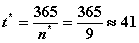день.