Какой вращающий момент действует на рамку с током?
Вспомним, что если какое-то тело может совершать вращение относительно произвольной оси О, то плечом силы относительно оси О называется расстояние от оси О до направления действия силы. На рис. 8.15 ось О «воткнута» в точке О, а все силы лежат в плоскости рисунка, плечо силы 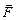 – ОА¢,
– ОА¢, 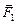 – ОВ¢,
– ОВ¢, 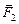 – ОС¢.
– ОС¢.
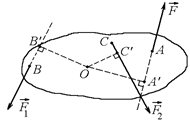 Рис. 8.15
Рис. 8.15
|
Подчеркнем, что плечо не является расстоянием от оси до точки приложения силы. Сила 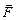 приложена в точке А,
приложена в точке А, 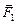 – в точке В,
– в точке В, 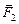 – в точке С.
– в точке С.
Иными словами, чтобы определить плечо силы относительно данной оси, надо провести прямую, вдоль которой действует сила, и опустить на эту прямую перпендикуляр из оси вращения.
Моментом силы относительно произвольной оси называется величина, равная произведению модуля силы на плечо, взятая со знаком «плюс», если сила стремится повернуть тело около данной оси по часовой стрелке, и со знаком «минус», если против. Так, на рис. 8.15:
момент силы 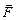 относительно точки О: МF = –|
относительно точки О: МF = –| 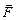 |×OA¢;
|×OA¢;
момент силы 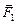 относительно точки О:
относительно точки О: 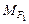 = –|
= –| 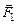 |×OВ¢;
|×OВ¢;
момент силы 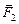 относительно точки О:
относительно точки О: 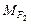 = +|
= +| 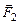 |×OС¢.
|×OС¢.
Момент пары сил
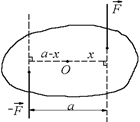 Рис. 8.16
Рис. 8.16
|
Пусть на некоторое тело действуют две равные по величине и противоположно направленные силы 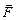 и –
и – 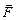 , причем расстояние между направлениями действия этих сил равно а. Определим момент пары сил относительно произвольной оси О (рис. 8.16).
, причем расстояние между направлениями действия этих сил равно а. Определим момент пары сил относительно произвольной оси О (рис. 8.16).
Пусть плечо силы 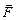 равно х, тогда плечо силы –
равно х, тогда плечо силы – 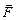 равно а – х. Поскольку обе силы вращают тело в одном направлении – по часовой стрелке, то их моменты положительны, а суммарный момент (момент пары) сил равен
равно а – х. Поскольку обе силы вращают тело в одном направлении – по часовой стрелке, то их моменты положительны, а суммарный момент (момент пары) сил равен
М = MF + M(–F) = F×x + F× (a – x) = F×x + F×a – F×x = F×a.
Следовательно, момент пары сил не зависит от того, относительно какой оси мы его считаем, и всегда равен произведению модуля силы 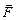 на расстояние а между направлениями их действия.
на расстояние а между направлениями их действия.
Если бы силы вращали тело против часовой стрелки, то момент пары сил имел бы знак «минус», но его величина Fa от этого бы не изменилась.
Теперь рассмотрим прямоугольную рамку с током I, находящуюся в однородном магнитном поле с индукцией 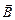 . Пусть горизонтальные стороны рамки равны b, а вертикальные а (рис. 8.17). Направление нормали
. Пусть горизонтальные стороны рамки равны b, а вертикальные а (рис. 8.17). Направление нормали 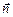 указывает направление магнитного поля, созданного током в самой рамке (по правилу буравчика или ППК). Вектор
указывает направление магнитного поля, созданного током в самой рамке (по правилу буравчика или ППК). Вектор 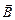 параллелен плоскости рамки.
параллелен плоскости рамки.
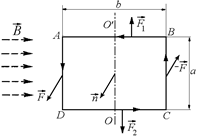 Рис. 8.17
Рис. 8.17
|
Силы 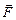 и –
и – 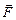 , действующие на вертикальные стороны рамки, образуют пару сил (рис. 8.18, а, вид сверху). Их вращающий момент по модулю равен
, действующие на вертикальные стороны рамки, образуют пару сил (рис. 8.18, а, вид сверху). Их вращающий момент по модулю равен
|M| = Fb.
(Так как силы 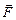 и –
и – 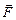 пытаются развернуть рамку против часовой стрелки, то М < 0. Но нас сейчас
пытаются развернуть рамку против часовой стрелки, то М < 0. Но нас сейчас
интересует только абсолютное значение момента.)
а 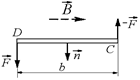 Рис. 8.18
Рис. 8.18
| б 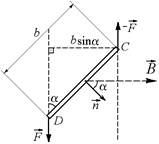
|
Поскольку по закону Ампера F = BIa, то |M| = BIab. А с учетом того, что площадь рамки S = ab, можем записать
|M| = BIS. (8.2)
Теперь рассмотрим ситуацию, когда нормаль к рамке 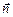 и вектор
и вектор 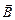 образует угол a (рис. 8.18, б, вид сверху). В этом случае силы
образует угол a (рис. 8.18, б, вид сверху). В этом случае силы 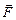 и –
и – 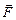 также образуют пару сил, только расстояние между направлением действия этих сил равно bsina. Тогда вращающий момент пары сил равен величине
также образуют пару сил, только расстояние между направлением действия этих сил равно bsina. Тогда вращающий момент пары сил равен величине
|M| = Fbsina = BIabsina = BISsina.
Запомним:
|M| = BISsina. (8.3)
Итак, мы установили важную зависимость: модуль вращающего момента сил, действующих на прямоугольную рамку с током в магнитном поле определяется формулой (8.3).
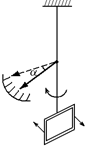 Рис. 8.19
Рис. 8.19
|
Заметим, что вращающий момент достаточно легко измерить с помощью крутильных весов. Крутильные весы схематически представляют собой нить со стрелкой, к которой подвешивают тело (например, рамку). На тело действуют силы, пытающиеся это тело повернуть (рис. 8.19). Поворачиваясь, тело закручивает нить. Такая деформация вызывает появление сил, стремящихся раскрутить нить в обратном направлении и обладающих, следовательно, вращающим моментом. Когда измеряемый момент становится равным моменту закрученной нити, установится равновесие.
Экспериментально установлено, что при небольших углах поворота вращающий момент нити прямо пропорционален углу поворота нити a: М ~ a. Поэтому, один раз измерив угол поворота нити при известном вращающем моменте, можно определить по углу поворота вращающий момент, который нужно измерить.
Читатель: А как определить вращающий момент сил, действующих на рамку произвольной формы, например, на рамку, имеющую форму треугольника или окружности?
Автор: Экспериментально установлено (а при большом желании это можно доказать теоретически), что на любую плоскую рамку площадью S с током I, расположенную в магнитном поле с индукцией 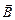 так, что векторы
так, что векторы 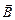 и
и 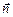 образуют угол a действует вращающий момент, вычисленный по формуле (8.3). Причем, как и в случае пары сил, величина этого момента одна и та же относительно любой оси вращения.
образуют угол a действует вращающий момент, вычисленный по формуле (8.3). Причем, как и в случае пары сил, величина этого момента одна и та же относительно любой оси вращения.
Еще один способ определения величины 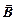
Формула (8.3) позволяет нам определить величину вектора 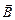 через вращающий момент. В самом деле, пусть в формуле (8.3) I = 1 A, S = 1 м2 и a = 90°, тогда |M| = В × 1× 1 × 1. То есть можно сказать, что величина вектора магнитной индукции численно равна модулю вращающего момента сил магнитного поля, действующих на плоскую рамку с током I = 1 А и площадью S = 1 м2, расположенную в магнитном поле так, что плоскость рамки параллельна направлению поля.
через вращающий момент. В самом деле, пусть в формуле (8.3) I = 1 A, S = 1 м2 и a = 90°, тогда |M| = В × 1× 1 × 1. То есть можно сказать, что величина вектора магнитной индукции численно равна модулю вращающего момента сил магнитного поля, действующих на плоскую рамку с током I = 1 А и площадью S = 1 м2, расположенную в магнитном поле так, что плоскость рамки параллельна направлению поля.
Читатель: Но тогда размерность В будет другой: из формулы (8.3) получим: 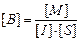 .
.
Автор: Размерность получается та же самая:
[B] = 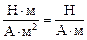 = Тл.
= Тл.
Задача 8.2. Проволочное кольцо с током находится в однородном магнитном поле, индукция которого В = 0,010 Тл. Сила тока в кольце I = 0,50 А. Радиус кольца R = 2,0 см. Какой максимальный момент сил может действовать на кольцо со стороны магнитного поля?
| В = 0,010 Тл I = 0,50 А R = 2,0 см = = 0,020 м | Решение. Максимальный вращающий момент возникает, когда плоскость рамки параллельна вектору 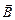 , т.е. когда нормаль к рамке составляет 90° с вектором , т.е. когда нормаль к рамке составляет 90° с вектором 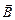 (см. рис. 8.17). Тогда по формуле (8.2) вращающий момент равен Mmax = BIS. В нашем случае S = pR2, тогда (см. рис. 8.17). Тогда по формуле (8.2) вращающий момент равен Mmax = BIS. В нашем случае S = pR2, тогда
|
| Мmax = ? | |
Mmax = BIpR2 » 0,010 Тл × 0,50 А × 3,14 × (0,020 м)2 » 6,3×10–6 Н×м.
Ответ: Mmax = BIpR2 » 6,3×10–6 Н×м.
СТОП! Решите самостоятельно: А11–А12, В13, С9.
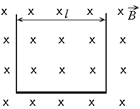 Рис. 8.20
Рис. 8.20
|
Задача 8.3.Между полюсами электромагнита в горизонтальном однородном магнитном поле с индукцией В = 0,050 Тл находится прямолинейный проводник массой т = 5,0 г и длиной l = 50 см, подвешенный горизонтально на гибких проводах под прямым углом к магнитному полю (см. рис. 8.20). Через проводник пропускают ток. При какой силе тока I исчезает натяжение проводов, поддерживающих проводник? В какую сторону должен при этом идти ток?
| В = 0,050 Тл т = 5,0 г = = 5,0×10–3 кг l = 50 см = = 0,50 м | Решение. Натяжение гибких проводов исчезает, если действующая на горизонтальный проводник сила Ампера Fa компенсирует силу тяжести mg. Из правила левой руки следует, что ток по проводнику должен идти слева направо (тогда сила Ампера направлена вверх). Поскольку Fa = IBl = = mg, получаем |
| I = ? | |
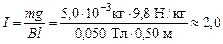 А.
А.
Ответ: 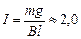 А, ток должен идти слева направо.
А, ток должен идти слева направо.
СТОП! Решите самостоятельно: В14, С10, С11, D3, D4.
Задача 8.4.Квадратная рамка с током помещена в однородное магнитное поле, индукция которого направлена вертикально. Рамка может вращаться вокруг горизонтальной стороны. Когда сила тока в рамке I = 5,0 А, рамка отклоняется от вертикальной плоскости на угол a = 30°. Площадь сечения проволоки рамки S = 4,0 мм2, а плотность материала провода r = 8,6×103 кг/м3. Определите индукцию магнитного поля.
| I = 5,0 А a = 30° S = 4,0 мм2 r = 8,6×103 кг/м3 | Решение. На каждую из сторон рамки действует сила тяжести 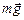 , приложенная к ее середине (рис. 8.21, а), где т = rSa.
На стороны АВ и CD действуют силы Ампера , приложенная к ее середине (рис. 8.21, а), где т = rSa.
На стороны АВ и CD действуют силы Ампера 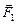 и и 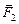 , лежащие в плоскости рамки и пытающиеся растянуть рамку. , лежащие в плоскости рамки и пытающиеся растянуть рамку.
|
| В = ? | |
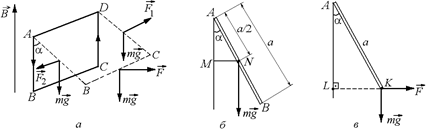
Рис. 8.21
На сторону ВС действует сила Ампера 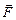 , пытающаяся повернуть рамку против часовой стрелки. Рамка находится в равновесии, если алгебраическая сумма моментов всех сил равна нулю.
, пытающаяся повернуть рамку против часовой стрелки. Рамка находится в равновесии, если алгебраическая сумма моментов всех сил равна нулю.
Моменты сил тяжести, действующих на стороны АВ и CD, равны (рис. 8.21, б, вид сбоку):
М1 = М2 = + mg × MN =
= mg 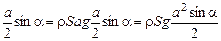 .
.
Момент силы тяжести, действующей на сторону ВС (рис. 8.21,в, вид сбоку) равен
М3 = + mg × LK = mgasina = rSagasina = rSga2sina.
Момент силы Ампера, действующей на сторону ВС, равен
M4 = –F × AL = –Facosa = –BIa× acosa = –BIa2cosa.
Моменты сил 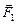 и
и 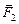 равны по величине и противоположны по направлению: сила
равны по величине и противоположны по направлению: сила 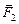 пытается повернуть рамку «на нас», а сила
пытается повернуть рамку «на нас», а сила 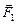 – «от нас». Моменты этих сил мы учитывать не будем.
– «от нас». Моменты этих сил мы учитывать не будем.
Запишем условие равновесия рамки:
М1 + М2 + М3 + М4 = 0 Þ
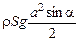 +
+ 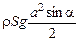 + rSga2sina + (–BIa2cosa) = 0 Þ
+ rSga2sina + (–BIa2cosa) = 0 Þ
 2rSga2sina = BIa2cosa Þ
2rSga2sina = BIa2cosa Þ
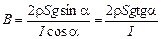 .
.
Подставим численные значения:
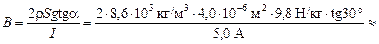
» 0,078 Тл.
Ответ: 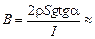 0,078 Тл.
0,078 Тл.
СТОП! Решите самостоятельно: С12, С13, D5, D6.
Дата добавления: 2016-04-11; просмотров: 7088;
