Чему равно гидростатическое давление?
Пусть в сосуде находится жидкость плотностью r. Попробуем найти разность давлений между двумя точками А и В, находящимися на одной вертикали, если расстояние между этими точками равно h (рис. 28.3,а).
 Мысленно выделим в жидкости тонкий вертикальный цилиндр, такой, что ось цилиндра проходит через точки А и В, и пусть точка А лежит на нижнем основании, а точка В – на верхнем основании цилиндра (рис. 28.3,б). Пусть площадь основания цилиндра равна S. Рассмотрим все силы, действующие на наш воображаемый цилиндр в вертикальном направлении.
Мысленно выделим в жидкости тонкий вертикальный цилиндр, такой, что ось цилиндра проходит через точки А и В, и пусть точка А лежит на нижнем основании, а точка В – на верхнем основании цилиндра (рис. 28.3,б). Пусть площадь основания цилиндра равна S. Рассмотрим все силы, действующие на наш воображаемый цилиндр в вертикальном направлении.
На верхнее основание со стороны жидкости действует сила давления FB = pBS, а на нижнее основание – сила давления FА = рАS. Кроме того, на цилиндр действует еще одна сила – сила тяжести цилиндра 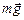 . Силы
. Силы 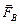 и
и 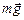 направлены вниз, а сила –
направлены вниз, а сила –  вверх. Так как вся жидкость, а значит, и наш цилиндр неподвижны, то равнодействующая сил, действующих на цилиндр в вертикальном направлении, равна нулю. Следовательно, сумма величин сил, направленных вниз, FB + mg равна величине силы, направленной вверх FA:
вверх. Так как вся жидкость, а значит, и наш цилиндр неподвижны, то равнодействующая сил, действующих на цилиндр в вертикальном направлении, равна нулю. Следовательно, сумма величин сил, направленных вниз, FB + mg равна величине силы, направленной вверх FA:
FA = FB + mg. (1)
Масса цилиндра т = rV, где V = Sh – объём цилиндра. Отсюда т = rSh. Подставляя значения FA, FВ и т в равенство (1), получим:
pAS = pВS +rShg.
Вынесем в правой части S за скобки
pAS = S (pВ +rhg)
и разделим обе части последнего равенства на S, получим:
pA = pВ +rhg.
Отсюда находим
pA – pВ = rhg. (28.1)
Заметим, что если точку В взять на поверхности жидкости, то давление жидкости в этой точке будет равно нулю: рВ = 0, а величина рА будет равна величине давления жидкости на глубине h:
p = rgh. (28.2)
Формула (28.2) позволяет рассчитывать гидростатическое давление в жидкости на глубине h. Заметим, что это давление зависит только от плотности жидкости r, напряженности гравитационного поля g и глубины h. От формы сосуда, в который налита жидкость, гидростатическое давление никак не зависит.
Задача 28.1. Сосуд с водой движется вертикально вверх с ускорением а. Найти давление на глубине Н. Плотность воды ρ.
| а Н ρ | Решение. Перейдем в н.с.о., связанную с сосудом. В этом случае на сосуд действуют силы 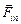 и и 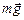 (рис. 28.4). Их равнодействующая (рис. 28.4). Их равнодействующая 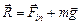 по модулю по модулю
|
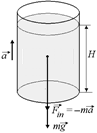 Рис. 28.4
Рис. 28.4
|
| р = ? | ||
равна 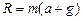 . Тогда можно считать, что сосуд находится в таких же условиях, как если бы он покоился, но ускорение свободного падения было бы равно . Тогда можно считать, что сосуд находится в таких же условиях, как если бы он покоился, но ускорение свободного падения было бы равно  . Отсюда давление на . Отсюда давление на
|
глубине Н
р = ρ g¢Н = ρ(g + a)Н.
Можно рассуждать и так: при движении с ускорением  , направленным вверх, вес воды возрастает и становится равным Р = =т(g +а),тогда давление
, направленным вверх, вес воды возрастает и становится равным Р = =т(g +а),тогда давление
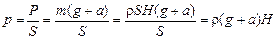 .
.
Ответ: р = ρ(g + a)Н.
СТОП! Решите самостоятельно: В7, С1, С2, С4.
Задача 28.2. В сообщающихся сосудах находится ртуть. Диаметр левого сосуда в четыре раза больше диаметра правого сосуда (рис. 28.5,а). В левый сосуд наливают столб воды высотой h0 = = 70 см. На сколько поднимется уровень ртути в правом сосуде и на сколько опустится в левом? ρв = 1,0 г/см3, ρр = 13,6 г/см3.
| d1 = 4d2 h0 = 70 см ρв = 1,0 г/см3 ρр = 13,6 г/см3 | 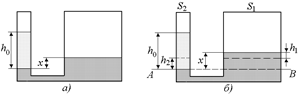 Рис. 28.5
Рис. 28.5
|
| h1 = ? h2 = ? | |
Решение.
1. Давление на уровне АВ в левом и правом сосудах равно, поэтому ρвgh0 = ρрgх.
2. При доливании воды часть ртути объема S2h2 перешла из левого сосуда в правый, объем ртути в котором увеличился на S1h1 (рис. 28.5,б). Отсюда S2h2 = S1h1.
3. Как видно из рис. 28.5,б, h1 + h2 = х.
4. Поскольку d1 = 4d2, то S1 = 16S2.
Объединим эти уравнения и получим систему:
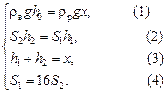
Подставляя (4) в (2), получим 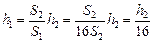 .
.
Подставляя h1 в (3), получим 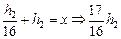 = х.
= х.
Подставим х в (1) и получим 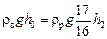 , откуда
, откуда
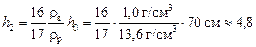 см,
см,
тогда  0,30 см.
0,30 см.
Ответ: в узком сосуде ртуть опустится на h2 = 4,8 см, в широком сосуде ртуть поднимется на h1 = 0,30 см.
СТОП! Решите самостоятельно: В9, В10, С8, С9.
Дата добавления: 2016-04-11; просмотров: 1829;
