Задачи средней трудности. В1. Хоккейная шайба, имея начальную скорость υ0 = 5,0 м/с, скользит до удара о борт площадки расстояние s =10 м
В1. Хоккейная шайба, имея начальную скорость υ0 = 5,0 м/с, скользит до удара о борт площадки расстояние s =10 м. Удар считать абсолютно упругим, коэффициент трения шайбы о лед k = 0,10, сопротивлением воздуха пренебречь. Определить, какой путь l пройдет шайба после удара.
В2. Во сколько раз уменьшится скорость атома гелия после центрального упругого столкновения с неподвижным атомом водорода, масса которого в четыре раза меньше массы атома гелия?
В3. Для получения медленных нейтронов их пропускают сквозь вещество, содержащие водород (например, парафин). Найти, какую наибольшую часть своей кинетической энергии нейтрон массы т0 может передать: а) протону (масса т0); б) ядру атома свинца (масса т = 207т0). Наибольшая часть передаваемой энергии соответствует упругому центральному удару.
Задачи трудные
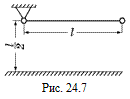 С1. Математический маятник, т. е. небольшой шарик нa тонкой нити, массой которой можно пренебречь, первоначально находится в горизонтальном положении. Длина нити маятника равна l. На расстоянии l/2 под точкой подвеса маятника расположена горизонтальная стальная плита. На какую высоту поднимется шарик после удара о плиту, если удар считать абсолютно упругим (рис. 24.7)?
С1. Математический маятник, т. е. небольшой шарик нa тонкой нити, массой которой можно пренебречь, первоначально находится в горизонтальном положении. Длина нити маятника равна l. На расстоянии l/2 под точкой подвеса маятника расположена горизонтальная стальная плита. На какую высоту поднимется шарик после удара о плиту, если удар считать абсолютно упругим (рис. 24.7)?
С2. Легкий шарик начинает свободно падать и, пролетев расстояние l, сталкивается упруго с тяжелой плитой, движущейся вверх со скоростью υ. На какую высоту h подскочит шарик после удара?
С3. Шарик движется между двумя очень тяжелыми вертикальными параллельными стенками, соударяясь с ними по закону абсолютно упругого удара. Одна из стенок закреплена, другая движется от нее с постоянной горизонтальной скоростью и2 = 0,5 м/с. Определить число соударений п и окончательную скорость υх шарика, если перед первым соударением со стенкой она была υ0х = 19,5 м/с. Соударения считать только с подвижной стенкой.
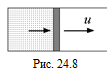 С4.В цилиндре, наполненном газом (рис. 24.8), поршень перемещается со скоростью и. Определить часть энергии, теряемую молекулой, скорость которой перпендикулярна к поверхности поршня, при столкновении с поршнем. Скорость молекулы равна υ (υ >> и). Столкновение молекулы с поршнем считать абсолютно упругим.
С4.В цилиндре, наполненном газом (рис. 24.8), поршень перемещается со скоростью и. Определить часть энергии, теряемую молекулой, скорость которой перпендикулярна к поверхности поршня, при столкновении с поршнем. Скорость молекулы равна υ (υ >> и). Столкновение молекулы с поршнем считать абсолютно упругим.
С5.Частица массы т1 налетает на покоящуюсячастицу массы т2 и после абсолютно упругого соударения отскакивает от нее в направлении, противоположном начальному. Во сколько раз изменится кинетическая энергия первой частицыв результате соударения, если h = (т2/т1) = 4,0?
С6.На шар, лежащий на гладкой горизонтальной поверхности, налетает другой шар такого же радиуса, движущийся горизонтально. Между шарами происходит упругий центральный удар. Построить график зависимости доли переданной энергии от отношения масс шаров х = m1/m2.
С7. Нейтрон испытывает упругое соударение с ядром гелия и затем, отразившись, упруго соударяется с другим ядром гелия (при упругих соударениях суммарная кинетическая энергия сохраняется). Ядра гелия до соударения были неподвижны. Считая оба соударения центральными (т.е. скорости до и после соударения направлены вдоль линии центра соударяющихся частиц), определить, во сколько раз изменится энергия нейтрона после двух соударений.
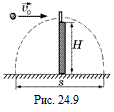 С8. Маленький шарик, летящий горизонтально со скоростью υ0 = 12 м/с, упруго ударяется о тело, лежащее на гладкой горизонтальной подставке на высоте Н (рис. 24.9). После удара оба тела упали на землю на расстоянии s = 10 м друг от друга. Найти Н.
С8. Маленький шарик, летящий горизонтально со скоростью υ0 = 12 м/с, упруго ударяется о тело, лежащее на гладкой горизонтальной подставке на высоте Н (рис. 24.9). После удара оба тела упали на землю на расстоянии s = 10 м друг от друга. Найти Н.
С9.Ha гладкой горизонтальной поверхности на некотором расстоянии от вертикальной стенки находится шар массы М. Другой шар, массы т, скользит с некоторой скоростью по направлению от стенки к первому шару. Между шарами происходит центральный упругий удар (при упругом ударе суммарная кинетическая энергия сохраняется). При каком соотношении масс М и m второй шар после удара достигнет стенки и, упруго отразившись от нее, догонит первый шар?
С10. Ha гладкой горизонтальной поверхности на расстоянии l = 3,0 м от вертикальной стенки находится шар массы М = 800 г. Другой шар массы т = 200 г скользит с некоторой скоростью по направлению от стенки к первому шару. Между шарами происходит центральный упругий удар. Второй шар после соударения достигает стенки и, упруго отразившись от нее, догоняет и вторично ударяет первый шар. Определить, на каком расстоянии от стенки произойдет второе соударение.
 С11. Несколько одинаковых стальных или костяных шаров подвешены на нитях, прикрепленных к одной доске (рис. 24.10). Шары в начальном положении касаются друг друга, и нити параллельны между собой. Если крайний правый шар отвести и отпустить, то после удара о неподвижные шары он останется в покое, а крайний левый шар отскочит. Если же отвести справа не один, а два шара и отпустить их одновременно, то слева отскочат тоже два. Как объяснить этот опыт?
С11. Несколько одинаковых стальных или костяных шаров подвешены на нитях, прикрепленных к одной доске (рис. 24.10). Шары в начальном положении касаются друг друга, и нити параллельны между собой. Если крайний правый шар отвести и отпустить, то после удара о неподвижные шары он останется в покое, а крайний левый шар отскочит. Если же отвести справа не один, а два шара и отпустить их одновременно, то слева отскочат тоже два. Как объяснить этот опыт?
С12. Как будет протекать опыт в задаче С11, если подвесить только три шарика и отвести в сторону два соседних шарика на одну и ту же высоту, затем отпустить их одновременно без начальной скорости?
С13. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Мaccы шаров т1 = 0,2 кг и т2 = 100 г. Первый шар отклоняют так, что его центр тяжести поднимается на высоту h = 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если удар: а) абсолютно упругий; б) абсолютно неупругий?
С14.Маятник представляет собой прямой тонкий стержень длины l = = 1,5 м, на конце которого находится стальной шар массой М = 1,0 кг. В шар попадает летящий горизонтально со скоростью υ = 50 м/с стальной шарик массы m = 20 г. Определить угол максимального отклонения маятника, считая удар упругим и центральным. Массой стержня пренебречь.
С15. Одинаковые упругие шарики массы т, подвешенные на нитях равной длины к одному крючку, отклоняют в разные стороны от вертикали на угол a и отпускают. Шарики ударяются и отскакивают друг от друга. Какова сила F, действующая на крючок: а) при крайних положениях нитей; б) в начальный и конечный моменты удара шариков; в) в момент наибольшей деформации шариков?
С16. На нити длины l = 2,0 м висит шарик массы т1 = 0,050 кг. Шарик касается шайбы, которая лежит на горизонтальной поверхности. Коэффициент трения между шайбой и полом k = 0,10. Нить с шариком отвели на угол 90° и отпустили. После упругого удара шарика о шайбу нить отклонилась обратно на угол a = 60°, а шайба прошла до остановки путь s. Найти массу шайбы и путь s.
С17. Шар массы т, движущийся со скоростью υ, налетает на покоящийся шар массы т/2 и после упругого удара продолжает двигаться под углом a = 30° к направлению своего первоначального движения. Найти скорости шариков после столкновения.
С18.Два шара А и В с различными неизвестными массами упруго сталкиваются между собой. Шар А до соударения находился в покое, а шар В двигался со скоростью υ. После соударения шар А приобрел скорость 0,50υ и начал двигаться под прямым углом к направлению своего первоначального движения. Определить направление движения шара А и его скорость υА после столкновения.
С19.При бомбардировке гелия a-частицами с энергией Е0 налетающая частица отклонилась на угол j = 60° по отношению к направлению ее движения до столкновения. Считая удар абсолютно упругим, определить энергии a-частиц Wa и ядра Wя после столкновения. Энергия теплового движения атомов гелия много меньше Е0.
С20.По гладкой горизонтальной поверхности навстречу друг другу скользят два одинаковых абсолютно упругих шара. Скорости шаров υ1 и υ2. С какими скоростями будут двигаться шары после центрального удара? Удар абсолютно упругий. Трение отсутствует.
С21.В покоящийся клин массы М попадает горизонтально летящая пуля массы т и после абсолютно упругого удара о поверхность клина отскакивает вертикально вверх (рис. 24.11). На какую высоту поднимется пуля, если горизонтальная скорость клина после удара оказалась равной υ? Трением пренебречь.
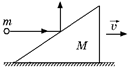 Рис. 24.11
Рис. 24.11 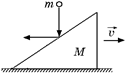 Рис. 24.12
Рис. 24.12
С22. На стоящий на горизонтальном полу клин массы М с высоты h падает шар массы т и отскакивает в горизонтальном направлении (рис. 24.12). Найти горизонтальную скорость υ клина после удара. Трением пренебречь. Удар о клин считать абсолютно упругим.
 Задача очень трудная
Задача очень трудная
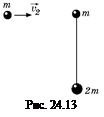
D1.На гладком горизонтальном столе лежат стальные шарики массами т и 2т, связанные натянутой нитью длины l. Еще один шарик массы т налетает на систему со скоростью υ0 (перпендикулярно натянутой нити) (рис. 24.13), и происходит абсолютно упругий лобовой удар. Найти максимальную величину натяжения нити и ускорение шарика массы 2т.
ЗАКОН СОХРАНЕНИЯ
Дата добавления: 2016-04-11; просмотров: 3527;
