Абсолютно упругий удар
При абсолютно упругом ударе тела после удара полностью восстанавливают свою форму, например, футбольный мяч при ударе о стену или биллиардные шары после столкновения. При этом суммарная кинетическая энергия взаимодействующих тел сохраняется.
Иными словами, кинетическая энергия не переходит во внутреннюю энергию взаимодействующих тел, и их температура не повышается.
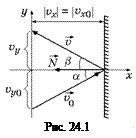 Рассмотрим абсолютно упругий удар шарика о массивную стену (рис. 24.1).
Рассмотрим абсолютно упругий удар шарика о массивную стену (рис. 24.1).
Пусть шарик подлетает к стене со скоростью 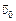 , составляющей угол a с нормалью к стене. Выясним, с какой скоростью
, составляющей угол a с нормалью к стене. Выясним, с какой скоростью 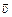 он отлетит от стены.
он отлетит от стены.
В момент удара о стену на шарик действует только сила нормальной реакции 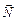 (силы трения быть не может, иначе выделялось ты тепло!).
(силы трения быть не может, иначе выделялось ты тепло!). 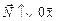 , Ny = 0, а значит, в вертикальном направлении тело не может получить ускорение: ау = 0, υ0у = υу.
, Ny = 0, а значит, в вертикальном направлении тело не может получить ускорение: ау = 0, υ0у = υу.
Поскольку при абсолютно упругом ударе общая кинетическая энергия сохраняется, а энергию, полученную стеной, в силу ее массивности можно считать равной нулю, то 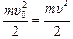 и υ = υ0. Но так как
и υ = υ0. Но так как 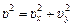 (по теореме Пифагора), то
(по теореме Пифагора), то 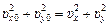 , а так как υ0у = υу, то |υ0х| = |υх|. Отсюда из равенства треугольников (см. рис. 24.1) следует, что угол отражения шарика b равен углу его падения a: a = b.
, а так как υ0у = υу, то |υ0х| = |υх|. Отсюда из равенства треугольников (см. рис. 24.1) следует, что угол отражения шарика b равен углу его падения a: a = b.
Итак, при абсолютно упругом ударе о массивную стену скорость тела не меняется по абсолютной величине, а угол падения равен углу отражения.
Задача 24.1. С высоты Н по гладкой наклонной плоскости длиной l = H/3 и углом наклона a = 30° соскальзывает без трения шарик и затем падает на горизонтальную плоскость, удар о которую следует считать абсолютно упругим (рис. 24.2,а). На какую высоту h поднимется шарик после удара о плоскость?
| Н l = H/3 a = 30° | а) 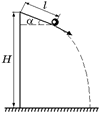 б) б) 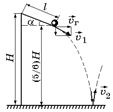
|
| h = ? | |
| Рис. 24.2 |
Решение. Чтобы найти h, рассмотрим движение шарика после удара о плоскость (рис. 24.2,б). Шарик движется как тело, брошенное под углом к горизонту, и высота подъема, как уже известно из кинематики, равна 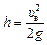 , где υв – вертикальная составляющая начальной скорости
, где υв – вертикальная составляющая начальной скорости 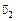 .
.
Найдем 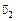 с помощью ТКЭ:
с помощью ТКЭ:
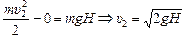 .
.
Чтобы найти горизонтальную составляющую скорости 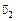 , найдем модуль скорости
, найдем модуль скорости 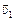 также с помощью ТКЭ:
также с помощью ТКЭ:
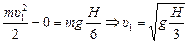 .
.
Из рис. 24.2,б:
υг = υ1cos30° = 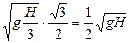 .
.
Заметим, что поскольку в горизонтальном направлении после отрыва от наклонной плоскости никакие силы на шарик не действуют, величина υг далее со временем не меняется и после удара о горизонтальную плоскость остается такой же, как после отрыва от наклонной плоскости.
Теперь найдем вертикальную составляющую скорости 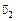 :
: 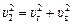 , где
, где 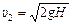 , υг =
, υг = 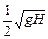 . Отсюда
. Отсюда
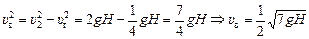 .
.
Тогда искомая высота равна 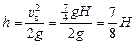 .
.
Ответ: 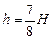 .
.
СТОП! Решите самостоятельно: В1, С1, С2.
Дата добавления: 2016-04-11; просмотров: 6653;
