Соударение маятников

Задача 24.3. Два упругих шарика подвешены на тонких нитях рядом так, что они находятся на одной высоте и соприкасаются (рис. 24.4,а). Нити подвеса разной длины: l₁ = 10 см, l₂ = 6,0 см. Массы шариков т₁ = 8,0 г и т₂ = 20 г соответственно. Шарик массы т₁ отклоняют на угол a = 60° и отпускают. Определить максимальное отклонение шариков от вертикали после удара. Удар считать абсолютно упругим.

l1 = 10 см l2 = 6,0 см т1 = 8,0 г т2 = 20 г a = 60°	Рис. 24.4
a1 = ? a2 = ?

Решение. Сначала найдем скорость υ первого шарика перед ударом. Воспользуемся ТКЭ (рис. 24.4,б): , где h = l₁ – –l₁cosa = l₁(1 – cosa). Отсюда

.

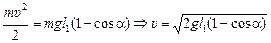Теперь найдем проекции скоростей шариков на ось х сразу после столкновения. Для этого воспользуемся формулой (24.1):

, ,

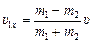где .

Так как т₁ < т₂, то направление 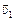противоположно направлению 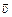. Иными словами, после удара шарик т₁ отскочит назад и поднимется на высоту , высота подъема второго шарика 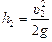. Углы a₁ и a₂ (рис. 24.5), на которые отклоняются первый и второй шарики после удара, определяются из треугольников АОВ и А¢О¢В¢:

; .

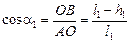Итак:

,

откуда

= ;

,

.

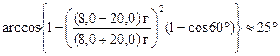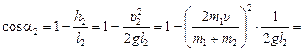
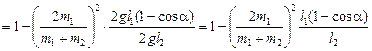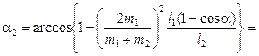
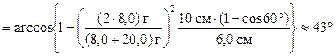Ответ: a₁ » 25°; a₂ » 43°.

СТОП! Решите самостоятельно: С11, С14, С16.