Последовательное соединение проводников

При последовательном соединении проводники как бы выстроены в цепочку: каждый проводник соединяется с одним предыдущим и одним последующим проводником (рис. 11.1).

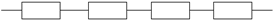Рис. 11.1

Напряжение на концах участка последовательно соединенных проводников равно сумме напряжений на каждом отдельном проводнике (рис. 11.2):

U = U₁ + U₂ + U₃ + ... + U_N. (11.1)

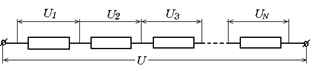Рис. 11.2

Читатель: А откуда это следует?

Автор: Вспомним, что напряжение на концах участка цепи численно равно работе, которую совершают силы электрического поля при перемещении единичного заряда с одного конца на другой. Напряже­ние на концах отдельного проводника численно равно работе по переме­щению единичного заряда через этот проводник.

Ясно, что для того чтобы перенести единичный заряд с одного конца участка, состоящего из последовательно соединенных проводников, на другой, нужно перенести этот заряд через каждый проводник данного участка. Поэтому полная работа по переносу заряда через N проводников равна сумме работ по перемещению заряда через каждый отдельный проводник.

При последовательном соединении проводников сила тока во всех проводниках одна и та же:

I₁ = I₂ = I₃ = ... = I_N = I. (11.2)

Читатель: А почему?

Автор: А давайте предположим, что это не так. Рассмотрим кусочек цепи, в котором проводник с номером i последовательно соединен с проводником под номером (i +1). Пусть сила тока в i-м проводнике не равна силе тока в (i +1)-м проводнике: I_i ¹ I_i+1 (рис. 11.3).

Рис. 11.3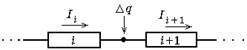

Положим для определенности: I_i > I_i+1. Тогда за время Dt из i-го проводника выходит заряд q_i = I_iDt, а в (i+1)-й провод­ник входит заряд q_i+1= I_i+1Dt.

Поскольку заряд исчезнуть не может, значит, между i-м и (i+1)-м проводниками заряд будет накапливаться. Величина этого заряда равна:

Dq = q_i – q_i+1 = I_iDt – I_i+1Dt = Dt(I_i – I_i+1).

Если взять промежуток времени Dt достаточно большим, то и величина Dq может стать сколь угодно большой. Ясно, что это невозмож­но. Значит, I_i = I_i+1.