Удельное сопротивление
Экспериментально установлено, что у провода длиной l и с площадью поперечного сечения S (рис. 10.15)электрическое сопротивление равно
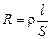 , (10.7)
, (10.7)
где ρ — физическая величина, зависящая только от свойств материала проводника, называемая удельным сопротивлением.
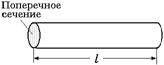 Рис. 10.15
Рис. 10.15
|
Единицы измерения удельного сопротивления. Из формулы (10.7)можно выразить ρ:
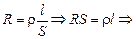
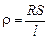 . (10.8)
. (10.8)
Тогда размерность ρ будет следующей: 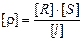 .
.
Если [R]= Ом, [S] = мм2, [l] = м, то 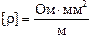 .
.
Физический смысл удельного сопротивления. Положим в формуле (10.8) S = 1 мм2, l = 1 м, тогда 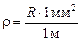 , т.е. удельное сопротивление численно равно электрическому сопротивлению провода, изготовленного из данного материала, длиной 1 м и с площадью поперечного сечения 1 мм2.
, т.е. удельное сопротивление численно равно электрическому сопротивлению провода, изготовленного из данного материала, длиной 1 м и с площадью поперечного сечения 1 мм2.
В табл. 10.1 приведены значения удельного сопротивления для некоторых материалов.
Читатель: А если площадь поперечного сечения измерять не в квадратных миллиметрах, а в квадратных метрах? Тогда единица измерения удельного сопротивления будет другой:
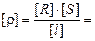
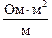 = Ом×м.
= Ом×м.
Автор: Вы правы, конечно. И такая единица измерения удельного сопротивления действительно существует.
Более того, именно эта единица измерения соответствует Международной системе единиц СИ. Другое дело, что такие провода, у которых площадь поперечного сечения было бы удобно измерять в квадратных метрах, встречается, прямо скажем, нечасто. Поэтому большее распространение получила внесистемная единица измерения (Ом×мм2)/м.
(Заметим, что час, минута, сутки, год – также внесистемные единицы измерения времени. В системе СИ основной единицей является секунда. Но вот килосекунды и мегасекунды на практике как-то не прижились.)
Т а б л и ц а 10.1
| Вещество | ρ,
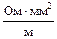
| Вещество | ρ,
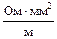
|
| Серебро (Ag) Медь (Сu) Алюминий (А1) Вольфрам (W) Платина (Pt) Железо (Fe) Сталь Свинец (Рb) Никелин (сплав Сr, Ni и Мn) Манганин (сплав Сu, Мn и Ni) Константан (сплав Сu и Ni) | 0,016 0,017 0,028 0,055 0,10 0,10 0,15 0,21 0,40 0,43 0,50 | Ртуть (Hg) Нихром (сплав Ni и Сr) Графит 10-% раствор серной кислоты (H2SO4) 10-% раствор поваренной соли (NaCl) 10-% раствор медного купороса (CuSO4) Древесина Мрамор Кварц плавленый | 0,96 1,1 2,5×104 8,3×104 3,15×105 1012 5×1013 5×1022 |
И все же в некоторых расчетах единица Ом×м более предпочтительна, поэтому найдем связь между Ом×м и (Ом×мм2)/м:
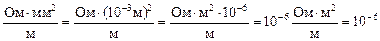 Ом×м.
Ом×м.
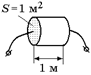 Рис. 10.16
Рис. 10.16
|
Например, для меди
ρ = 0,017 (Ом×мм2)/м = 0,017×(10–6 Ом×м) =
= 0,017×10–6 Ом×м = 1,7×10–8 Ом×м.
Это значит, что если мы возьмем проволоку, имеющую форму цилиндра с площадью основания S = 1 м2 и высотой l = 1 м (рис. 10.16) и подадим напряжение на противоположные грани этой специфической проволоки, то ее сопротивление будет равно 1,7×10–8 Ом.
Заметим, что вообще сопротивление массивных проводников (то есть имеющих большие поперечные сечения) – величины исчезающе малые.
Зависит ли сопротивление от температуры? Оказывается, зависит. Экспериментально установлено, что с повышением температуры удельное сопротивление практически у всех металлов повышается. У электролитов же, наоборот, с ростом температуры удельное сопротивление уменьшается.
Задача 10.3. Найти сопротивление R медной проволоки, масса которой т = 1,0 кг, а площадь поперечного сечения S = 0,10 мм2. Плотность меди g = 8,9×103 кг/м3, ее удельное сопротивление r = = 0,017 мкОм×м.
| т = 1,0 кг S = 0,10 мм2 = 1,0×10–7 м2 g = 8,9×103 кг/м3 r = 0,017 мкОм×м = = 1,7×10–8 Ом×м. | Решение.
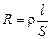 , (1)
т = gSl Þ , (1)
т = gSl Þ 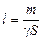 Þ (1) Þ Þ (1) Þ 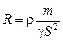 .
Подставим численные значения .
Подставим численные значения
|
| R = ? |
R = 1,7×10–8 Ом×м 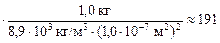 Ом » 0,19 кОм.
Ом » 0,19 кОм.
Ответ: 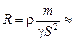 0,19 кОм.
0,19 кОм.
СТОП! Решите самостоятельно: А6, В7, В8, В10, В11, С3.
Задача 10.4.Удельное сопротивление графитового стержня от карандаша r = 400 мкОм×м. Какой ток I пройдет по стержню, если на него подать напряжение U = 6,0 В? Длина стержня l = 20 см, его диаметр D = 2,0 мм.
| r = 400 мкОм×м = = 4,00×10–4 Ом×м U = 6,0 В l = 20 см = 0,20 м D = 2,0 мм = 2,0×10–3 м | Решение.
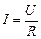 , (1) , (1)
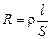 , (2) , (2)
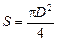 . (3) . (3)
|
| I = ? | |
Подставив (3) в (2), получим 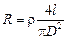 , теперь подставим это значение в (1):
, теперь подставим это значение в (1): 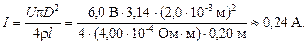
Ответ: 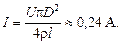
СТОП! Решите самостоятельно: В12, В13, С5.
Дата добавления: 2016-04-11; просмотров: 1869;
