Взаимодействие трех и более зарядов
Читатель: Предположим, что три заряда (+q, +q и +q) расположены на одной прямой (рис. 2.1) Расстояние между соседними зарядами равно а. Можно ли утверждать, что заряд 1 действует на заряд 3 с силой, определяемой законом Кулона 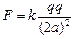 ? Ведь между ними есть еще заряд 2, который может как-то помешать взаимодействию зарядов 1 и 3.
? Ведь между ними есть еще заряд 2, который может как-то помешать взаимодействию зарядов 1 и 3.
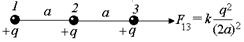 Рис. 2.1
Рис. 2.1
Автор: Экспериментально установлено, что сила взаимодействия двух зарядов не изменяется, если вблизи них поместить еще какие-либо заряды.
Пусть имеются заряд q и заряды q1, q2, q3,…, qN. Тогда результирующая сила 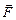 , с которой действуют на заряд q все N зарядов qi, определяется формулой
, с которой действуют на заряд q все N зарядов qi, определяется формулой
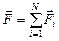 , (2.1)
, (2.1)
где 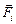 – сила, с которой действует на заряд q заряд qi в отсутствии остальных (N – 1)-го зарядов.
– сила, с которой действует на заряд q заряд qi в отсутствии остальных (N – 1)-го зарядов.
Задача 2.1. На одной прямой находятся заряды (–2q), +2q и +q. Расстояние между соседними зарядами а. Найти величину результирующей силы, действующей на заряд +q.
| (–2q), +2q, +q а | Решение. Введем ось х (рис. 2.2).
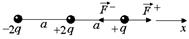 Рис. 2.2 Рис. 2.2
|
|  | = ? | = ?
|
Согласно формуле (2.1) результирующая сила 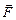 , действующая на заряд +q, равна
, действующая на заряд +q, равна 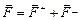 .
.
В проекции на ось х
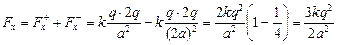 .
.
Так как 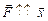 , то
, то 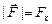 .
.
Ответ: 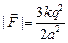 .
.
СТОП! Решите самостоятельно: В1–В3, С1.
Задача 2.2. Два положительных заряда q и 2q закреплены неподвижно на расстоянии а друг от друга. На каком расстоянии от заряда q следует разместить заряд Q, чтобы он находился в положении равновесия?
| q 2q Q a | Решение. Введем ось х (рис. 2.3).
Рис. 2.3 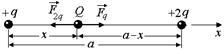 Запишем условие равновесия для заряда Q в проекции на ось х:
Запишем условие равновесия для заряда Q в проекции на ось х:
|
| x = ? | |
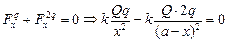 .
.
Решим это уравнение относительно х:
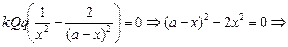
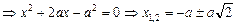 ;
;
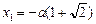 ;
; 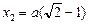 .
.
Отрицательный корень мы отбрасываем: если заряд Q окажется левее заряда q, то в положении равновесия он находиться не сможет.
Ответ: 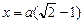 .
.
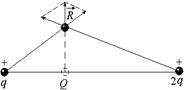 Рис. 2.4
Рис. 2.4
| Читатель: Устойчиво ли это равновесие? Автор: Вообще говоря, нет. Если сместить заряд Q чуть-чуть перпендикулярно оси х, возникнут силы, удаляющие его от положения равновесия (рис. 2.4). |
Читатель: А если заряду Q разрешить двигаться только вдоль оси х (например, посадив все заряды на гладкую проволоку)?
Автор: Тогда положение равновесия устойчиво. Допустим, мы сместились из положения равновесия вправо в точку 1 (рис. 2.5). Тогда сила вдоль оси х (со стороны заряда +q) уменьшилась, а сила против оси х (со стороны заряда +2q) возросла. Значит, равнодействующая будет направлена против оси х, и заряд Q вернется в положение равновесия. То же будет при попытке сместить заряд влево от положения равновесия в точку 2.
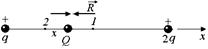 Рис. 2.5
Рис. 2.5
СТОП! Решите самостоятельно: В4, В5, С2.
Задача 2.3. Два положительных заряда +q находятся на расстоянии а друг от друга. Найти результирующую силу, с которой они действуют на такой же заряд +q, равноудаленный на расстояние а от каждого заряда.
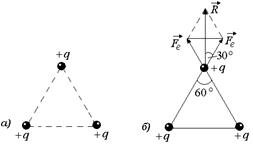 Рис. 2.6 Рис. 2.6
| |
| q a | |
| R = ? | |
Решение. Все заряды находятся в вершинах правильного треугольника (рис. 2.6,а). Из симметрии задачи легко видеть, что результирующая сила направлена вертикально вверх (рис. 2.6,б), причем ее модуль равен 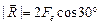 , где
, где 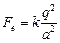 . Отсюда
. Отсюда
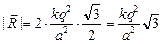 .
.
Ответ: 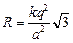 .
.
СТОП! Решите самостоятельно: В8, В9, С7.
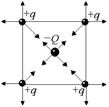
Задача 2.4. В четырех вершинах квадрата находятся одинаковые заряды q > 0. Какой заряд надо поместить в центр, чтобы система находилась в положении равновесия?
| q | Решение. Ясно, что заряд в центре системы должен быть отрицательным (рис. 2.7,а). Из симметрии задачи очевидно, что при любых значениях q заряд Q всегда будет в равновесии, а вот заряд q – не всегда. | |
| Q = ? | ||
Запишем условие равновесия для одного из зарядов q: 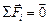 .
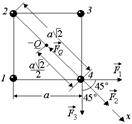
Пусть сторона квадрата равна а (рис. 2.7,б). Тогда диагональ квадрата равна .
Пусть сторона квадрата равна а (рис. 2.7,б). Тогда диагональ квадрата равна 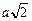 , половина диагонали , половина диагонали 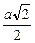 . Введем ось х вдоль диагонали и запишем 2-й закон Ньютона в проекции на эту ось: . Введем ось х вдоль диагонали и запишем 2-й закон Ньютона в проекции на эту ось:
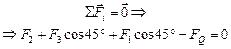 . (1)
Здесь . (1)
Здесь 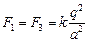 ; ; 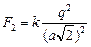 ; ; 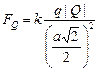 . .
|
 а
а
 б
Рис. 2.7
б
Рис. 2.7
| |
Подставим эти значения в формулу (1):
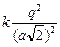 +
+ 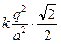 +
+ 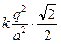 –
– 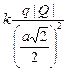 = 0,
= 0,
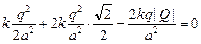 ,
, 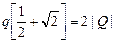 ,
,
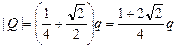 .
.
Поскольку Q < 0, то 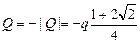 .
.
Ответ: 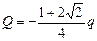 .
.
СТОП! Решите самостоятельно: С4, С10, С14.
Задача 2.5. По кольцу радиуса R, расположенному вертикально в поле тяжести Земли, могут без трения скользить одинаковые шарики массы т. Один шарик закреплен в верхней точке кольца. Два подвижных шарика имеют заряды, равные q. Найти заряд закрепленного шарика, если известно, что все шарики оказались в вершинах правильного треугольника.
| q | Решение. Так как силы трения нет, сила нормальной реакции направлена по радиусу (рис. 2.8). | |
| Q = ? | ||
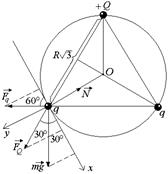 Рис. 2.8
Рис. 2.8
| Если незаряженный шарик неподвижен на кольце, значит, сумма проекций всех сил, действующих на него, на ось х, направленную по касательной к окружности, равна нулю.
Если радиус окружности R, то сторона вписанного треугольника а = = 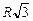 . Запишем 2-й закон Ньютона в проекции на ось х для шарика с зарядом q:
mgx + FQx + Fqx = 0, . Запишем 2-й закон Ньютона в проекции на ось х для шарика с зарядом q:
mgx + FQx + Fqx = 0,
| |
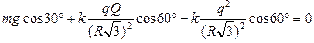 ,
,
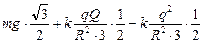 = 0,
= 0,
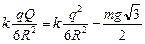 ,
,
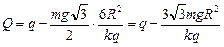 .
.
Ответ: Q = 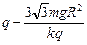 .
.
СТОП! Решите самостоятельно: С13(1), С13(3), С12.
Дата добавления: 2016-04-11; просмотров: 12702;
