Единицы измерения заряда
В системе СИ заряд измеряется в кулонах (Кл). Кулон – это производная единица от основной единицы измерения тока в СИ – ампера (А). За 1 кулон принят заряд, который проходит через поперечное сечение проводника за 1 секунду, если по нему течет ток в 1 ампер. То есть так как q = I×t, то 1 Кл = 1 А×с.
Если заряд измерять в кулонах, силу – в ньютонах, а расстояние в метрах, то коэффициент пропорциональности в законе Кулона равен k = 9×109 (Н×м2)/Кл2 (это экспериментальный факт). Размерность k легко получается из формулы (1.2):
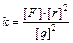 .
.
Итак, в СИ закон Кулона имеет вид
F = 9×109 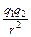 . (1.4)
. (1.4)
Задача 1.1. С какой силой притягиваются два разноименных точечных заряда величиной q = 1,0 Кл каждый, находящиеся на расстоянии r = 1,0 км друг от друга?
| q = 1,0 Кл r = 1,0 км | Решение.
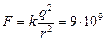 (Н×м2)/Кл2 × (Н×м2)/Кл2 × 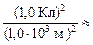 » 9,0×103 Н = 9,0 кН.
» 9,0×103 Н = 9,0 кН.
|
| F = ? | |
Ответ:  9,0 кН.
9,0 кН.
Как видим, величина заряда в 1 Кл очень велика, а решенная нами задача носит чисто теоретический характер: получить заряд в 1 Кл на одном небольшом теле невозможно!
Задача 1.2. Два заряда, каждый из которых состоит из М = 1,0 г электронов, находятся на расстоянии r = 1,0 км. Найти величину каждого заряда и силу их взаимодействия. Заряд электрона е = =1,6×10–19 Кл, масса электрона те = 9,1×10–31 кг.
| М = 1,0×10–3 кг r = 1,0×103 м е = 1,6×10–19 Кл те = 9,1×10–31 кг | Решение.
 » 1,8×108 Кл.
» 1,8×108 Кл.
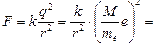
|
| q = ? F = ? | |
 Н.
Н.
Ответ: 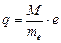 » 1,8×108 Кл;
» 1,8×108 Кл; 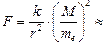 2,8×1020 Н.
2,8×1020 Н.
Заметим, что собрать в одном месте столько электронов вряд ли удастся (уж очень они легкие и 1 г электронов – это очень много!).
СТОП! Решите самостоятельно: А7, А15, В5, В8.
Задача 1.3. Сколько электронов содержит кусок железа массой т = 1,0 кг? Заряд ядра атома железа z = 26.
| т = 1,0 кг z = 26 | Решение. Массовое число железа равно 56, значит, m = 0,056 кг/моль.
пе = z × (число атомов) = 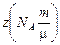 =
= =
= 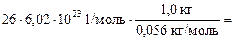 2,8×1026 (шт.) 2,8×1026 (шт.)
|
| пе = ? | |
Ответ: пе = 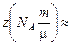 2,8×1026.
2,8×1026.
СТОП! Решите самостоятельно: А4, В1, В3.
Кроме СИ, существует ещесистема единиц СГС (сантиметр–грамм–секунда). В этой системе основными являются три единицы: 1 см, 1 г, 1 с. Все остальные единицы – производные. Например:
скорость [υ] = см/с,
ускорение [a] = см/с2,
сила [F] = [m][a] = (г×см)/с2 = дина,
работа [A] = [F][l] = дина×см = эрг.
В системе СГС коэффициент k в законе Кулона (1.2) полагается равным 1, и закон Кулона имеет вид
 . (1.5)
. (1.5)
Отсюда легко получить единицу измерения заряда:
 .
.
Такая удивительная единица называется единицей измерения заряда в СГС и обозначается так: 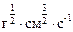 = СГСЭq.
= СГСЭq.
Задача 1.4. Два одинаковых заряда q = 1 СГСЭq находятся на расстоянии r = 1 см друг от друга. Какова сила их взаимодействия в СИ и в СГС?
| q = 1 СГСЭq r = 1 см | Решение.
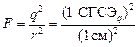 =1 дина.
Выразим дину в ньютонах: =1 дина.
Выразим дину в ньютонах:
|
| F = ? | |
1 дина =  .
.
Ответ: 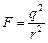 = 1 дина = 1×10–5 Н.
= 1 дина = 1×10–5 Н.
СТОП! Решите самостоятельно: В14, С4.
Выясним, как связаны между собой две единицы измерения заряда: 1 Кл и 1 СГСЭq. Возьмем два заряда в 1 Кл и разместим их на расстоянии 1 м = 100 см. Тогда сила взаимодействия между ними будет
F = 9×109 Н = 9×109×(105 дин) = 9×1014 дин.
В системе СГС закон Кулона в этом случае будет иметь вид
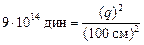 ,
,
где q – заряд, равный заряду в 1 Кл, но в единицах СГС:
q2 = 9×1014 дин×104 см2 = 9×1018 дин×см2.
Отсюда
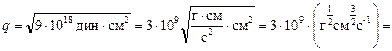
= 3×109 СГСЭq.
Но поскольку q = 1 Кл (так мы положили в самом начале наших рассуждений), то
1 Кл = 3×109 СГСЭq. (1.6)
Заметим, что в СИ закон Кулона часто записывают в виде
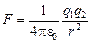 , (1.7)
, (1.7)
т.е. представляют коэффициент k = 9×109 (Н×м2)/Кл2 в виде
k = 9×109 (Н×м2)/Кл2 = 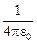 ,
,
откуда
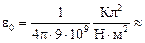 8,84×10–12 Кл2/(Н×м2).
8,84×10–12 Кл2/(Н×м2).
Эта величина называется электрической постоянной.
В чем смысл такой замены? В удобстве. Но это удобство с первого взгляда представляется лишь дополнительным неудобством. Поэтому до поры до времени будем писать закон Кулона в виде  , где k = 9×109 (Н×м2)/Кл2.
, где k = 9×109 (Н×м2)/Кл2.
Задача 1.5. Два маленьких одинаковых проводящих шарика, имеющих заряды q1 и q2, привели в соприкосновение. Найти заряд на каждом шарике после соприкосновения. Рассмотреть случаи, когда заряды q1 и q2 имеют одинаковые и разные знаки.
| q1 q2 | Решение. 1. Пусть заряды одного знака: q1 > 0, q2 > 0 или q1 < 0, q2 < 0. Тогда суммарный заряд двух шариков по величине равен |Q| = |q1| + |q2|. |
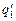 , , 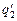 = ? = ?
| |
В силу симметрии задачи он распределяется поровну между шариками:
 .
.
Если q1 > 0 и q2 > 0, то 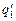 =
= 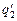 =
=  .
.
Если q1 < 0 и q2 < 0, то
– 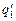 = –
= – 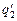 =
= 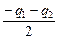 Þ
Þ 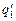 =
= 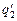 =
=  .
.
2. Пусть заряды q1 и q2 – разных знаков. Для определенности положим: q1 > 0, q2 < 0.
Если |q1| > |q2|, тогда общий заряд шариков Q = |q1| – |q2| > 0. В силу симметрии
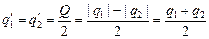 .
.
Если |q1| < |q2|, тогда общий заряд шариков Q = |q2| – |q1| < 0. В силу симметрии
 .
.
Итак, при любых знаках зарядов q1 и q2 и любых соотношениях между величинами зарядов q1 и q2 после соприкосновения на шариках будут равные заряды: 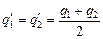 .
.
СТОП! Решите самостоятельно: В7, В17, В18, С3.
Задача 1.6. На тонкой нерастяжимой нити висит шарик массой т и зарядом q1. Снизу на расстоянии l под ним по вертикали располагают шарик с зарядом q2. Найти силу натяжения нити, если первый шарик остается неподвижным.
| q1, q2 l, m | Решение.
1. Пусть (q1q2) < 0, т.е. шары притягиваются (рис. 1.5). Тогда 2-й закон Ньютона в проекции на ось у будет иметь вид
у: Т – mg – 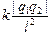 = 0.
Отсюда
Т = mg + = 0.
Отсюда
Т = mg + 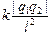 .
2. Пусть (q1q2) > 0, т.е. шары отталкиваются. Тогда .
2. Пусть (q1q2) > 0, т.е. шары отталкиваются. Тогда
|
| T = ? | |
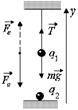 Рис. 1.5
Рис. 1.5
|
у: Т – mg + 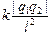 = 0 Þ Т = mg –
= 0 Þ Т = mg – 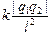 .
.
В первом случае |q1q2| = –q1q2, а во втором |q1q2| = +q1q2, поэтому в общем случае справедлива формула
Т = mg – 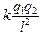 .
.
Это и есть ответ задачи.
СТОП! Решите самостоятельно: В30, В31, С14.
Задача 1.7. Два одинаковых шарика массой т подвешены на тонких нерастяжимых нитях в одной точке. Какой угол с вертикалью составят нити, если сообщить шарикам равные положительные заряды q? Расстояние между шариками равно R.
| q т R | Решение. Запишем 2-й закон Ньютона в проекциях на оси х и у (рис. 1.6): | |
х: Fe – Tsina = 0;
y: –mg + Tcosa = 0.
Fe = 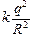 , тогда , тогда
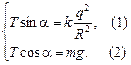
| 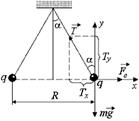 Рис. 1.6
Рис. 1.6
| |
| a = ? | ||
Разделив уравнение (1) на уравнение (2), получим
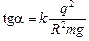 ,
,
отсюда
 .
.
Ответ:  .
.
СТОП! Решите самостоятельно: В21, В25, С7, С8.
Задача 1.8. Два одинаковых шарика массой т и зарядом q > 0каждый, связанные тонкой нерастяжимой нитью длиной l, движутся под действием силы F, как показано на рис. 1.7. Найти ускорение шариков и силы натяжения нитей.
| q т l F | 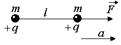 Рис. 1.7
Решение.
1. Рассмотрим систему как целое. Тогда 2-й закон Ньютона в проекции на ось х (рис. 1.8) имеет вид
х: F = 2ma Þ Рис. 1.7
Решение.
1. Рассмотрим систему как целое. Тогда 2-й закон Ньютона в проекции на ось х (рис. 1.8) имеет вид
х: F = 2ma Þ 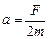 . .
| |
| a = ? Т = ? | ||
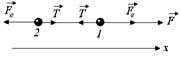 Рис. 1.8
Рис. 1.8
| 2. Теперь рассмотрим шар 2 как отдельное тело и, применив к нему 2-й закон Ньютона, получим Т – Fe = та, отсюда | |
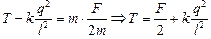 .
.
Ответ: 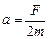 ;
;  .
.
СТОП! Решите самостоятельно: С16, С17.
Задача 1.9. Три шарика массой т каждый связаны тонкими нерастяжимыми нитями и движутся вертикально вверх в поле тяжести земли под действием силы F так, что нити между собой образуют угол a = 60° (рис. 1.9). Найти силы натяжения нитей, ускорение системы и длины нитей, если два нижних шарика имеют одинаковые положительные заряды q.
| a = 60° q т F | 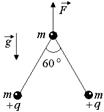 Рис. 1.9
Рис. 1.9
| Решение.
1. Рассмотрим систему как целое. Тогда в проекции на ось у (рис. 1.10) 2-й закон Ньютона имеет вид F – 3mg = 3ma. Отсюда
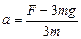 . (1) . (1)
|
| l = ? Т = ? а = ? | ||
2. Рассмотрим шарик 1 (рис. 1.10) и запишем 2-й закон Ньютона в проекциях на оси х и у:
х: Fe – Tsin30° = 0;
y: Tcos30° – mg = ma.
Отсюда
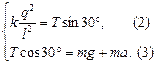 Подставив (1) в (3), получим
Подставив (1) в (3), получим
| 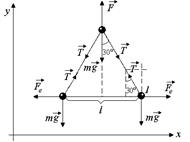 Рис. 1.10
Рис. 1.10
|
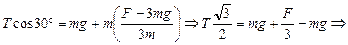
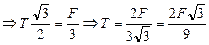 .
.
Теперь подставим значение Т в уравнение (2):

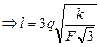 .
.
Ответ: 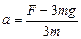 ;
;  ;
; 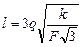 .
.
СТОП! Решите самостоятельно: С18, С19.
Задача 1.10. В модели атома водорода Бора электрон вращается вокруг ядра с постоянной скоростью. Найти скорость вращения электрона, если радиус вращения ядра r = 1,0×10–10 м.
| r = 1,0×10–10 м т = 9,1×10–31 кг q = 1,6×10–19 Кл | Решение. Сила притяжения ядра сообщает электрону центростремительное ускорение
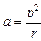 ,
направленное к центру орбиты (рис. 1.11), тогда ,
направленное к центру орбиты (рис. 1.11), тогда
|
| υ = ? | |
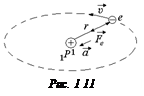

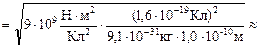
» 1,6×106 м/с.
Ответ: 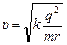 » 1,6×106 м/с.
» 1,6×106 м/с.
СТОП! Решите самостоятельно: В26, В28.
Задача 1.11. Тело массой т вращается на нити длиной l, образуя конический маятник около точечного заряда, расположенного в центре окружности. Угловая скорость w. Найти величину заряда тела, если известно, что он равен величине точечного заряда, помещенного в центре окружности.
| w a т l | Решение. Запишем 2-й закон Ньютона в проекциях на оси х и у (рис. 1.12):
х: Tsina – Fe = mw2r;
у: Tcosa – mg = 0.
Из треугольника ОО1А имеем r = lsina. Закон Кулона Fe = 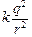 . Отсюда получим . Отсюда получим
 Подставляя значение Т из (1) в (2), найдем q:
Подставляя значение Т из (1) в (2), найдем q:
|
| q = ? | |
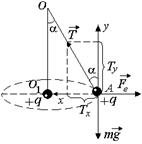 Рис. 1.12
Рис. 1.12
|
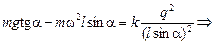
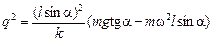 .
.
Отсюда получаем ответ:
 .
.
СТОП! Решите самостоятельно: В29, С12, С13.
Дата добавления: 2016-04-11; просмотров: 2322;
