Ошибка разности между средними арифметическими двух вариационных рядов.
В экспериментальной и практической работе большое значение имеет определение разности между средними показателями двух сравниваемых групп животных и установление достоверности этой разности.
Например, часто требуется определить, достоверна ли прибавка удоя при введении в рацион коров какого-либо кормового компонента.
В ветеринарных исследованиях очень важно бывает доказать, что примененная доза или новый лекарственный препарат достоверно уменьшает долю заболевших животных по сравнению с долей больных животных в контрольной группе, не подвергавшихся лечению.
Определение достоверности разности между средними арифметическими или долями двух вариационных рядов можно определить с помощью ошибки разности md
Формула ошибки разности следующая: 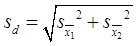 ,
,
где 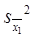 - квадрат ошибки средней арифметической 1-го вариационного ряда,
- квадрат ошибки средней арифметической 1-го вариационного ряда, 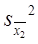 - квадрат ошибки средней арифметической 2-го вариационного ряда,
- квадрат ошибки средней арифметической 2-го вариационного ряда,
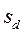 - искомая ошибка разности.
- искомая ошибка разности.
Эта формула используется в тех случаях, когда варианты одной выборки некоррелированы с вариантами другой выборки.
Критерий достоверности разности между средними арифметическими вычисляют по следующей формуле
Найденный критерий td сравнивают с табличным значением критерия Стъюдента при числе степеней свободы k=n1+n2-2, где n1 и n2 — объемы выборок.
Если td< tst - разность считается недостоверной. Это значит, что не получено никакого определённого ответа о разности между соответствующими генеральными параметрами. Если получена благоприятная по смыслу исследования разность между двумя выборочными средними, но эта разность оказалась недостоверной, то это значит, что между соответствующими генеральными средними могут быть любые соотношения, а какие именно неизвестно, но это не может служить доказательством отсутствия разницы между генеральными средними.
Если в выборочном исследовании оказалась достоверная разница между выборочными показателями, то такая же разница по знаку будет и между соответствующими генеральными параметрами. Основной вывод может быть перенесён на генеральную совокупность.
Для коррелированных выборок используется следующая формула разности между средними: 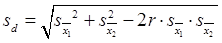 ,
,
где s1 и s2 – ошибки средних арифметических по каждой выборке;
r – коэффициент корреляции между вариантами обеих выборок при попарном их сопоставлении.
Пример. При определении доли влияния системы содержания на конверсию корма на 1 кг прироста живой массы бройлеров различных кроссов было отмечено, что лучший генетический потенциал по данному показателю по всем кроссам выявлен у молодняка, выращенного в реконструированных птичниках с регулируемым микроклиматом (см. табл.). Определим достоверность различий в показателях по конверсии корма на 1 кг прироста живой массы бройлеров при разных системах содержания. Сравнение проведём с данными при содержании бройлеров в реконструированных птичниках с регулируемым микроклиматом.
Вычислим критерий достоверности разности между средними арифметическими для кросса «Смена-4»
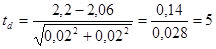
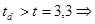 различие достоверно при уровне значимости P<0,001
различие достоверно при уровне значимости P<0,001
Для кросса «Кобб-500»
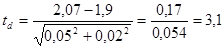
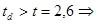 различие достоверно при уровне значимости P<0,01
различие достоверно при уровне значимости P<0,01
Для кросса «Арбор-Айкрес"
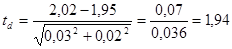
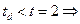 различие недостоверно
различие недостоверно
Таблица. Конверсия корма на 1 кг прироста живой массы высокопродуктивных бройлеров при разных системах содержания.
| Кросс | Система содержания | ||||||||
| Напольная на глубокой подстилке | Клеточная (в батареях типа БКМ-3Б) | Напольная в реконструированных птичниках | |||||||
| 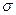
| 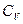 % %
| 
| 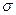
| 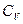 % %
| 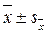
| 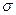
| 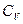 % %
| |
| СМЕНА-4 | 2,17
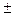 0,01*** 0,01***
| 0,11 | 5,0 | 2,2 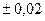 ***
***
| 0,07 | 3,2 | 2,06
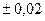
| 0,10 | 4,8 |
| ИЗА | 1,99 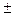 0,01***
0,01***
| 0,10 | 4,3 | 2,05
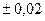 *** ***
| 0,10 | 3,4 | 1,90
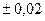
| 0,06 | 3,2 |
| РОСС-308 | 2,07 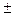 0,02 0,02
| 0,12 | 4,8 | 2,10
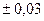
| 0,08 | 3,8 | 2,03
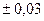
| 0,09 | 4,4 |
| КОББ-500 | 1,97 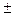 0,02*
0,02*
| 0,10 | 5,1 | 2,07
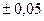 ** **
| 0,15 | 7,2 | 1,90
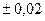
| 0,07 | 3,7 |
| АРБОР АЙКРЕС | 2,02 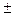 0,02*
0,02*
| 0,13 | 4,9 | 2,02
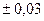
| 0,10 | 4,9 | 1,95
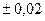
| 0,03 | 1,5 |

*/ Достоверно выше по сравнению с напольным содержанием в реконструированных птичниках с регулируемым микроклиматом при Р<0,05;
**/ при Р<0,01;
***/ при Р<0,001
Ошибки для выборочных показателей ( 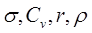 )
)
Обозначим ошибку буквой m
Статистические ошибки для 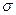 и Cv выражаются следующими формулами:
и Cv выражаются следующими формулами:
— ошибка среднего квадратического отклонения,
— ошибка коэффициента вариации.
Критерий достоверности определяют обычным методом:
Величину t определяют для трёх уровней вероятности: 0,95; 0,99; 0,999,
которые определяют по таблице Стьюдента.
Критерии достоверности разности между 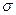 и
и 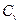 определяются по следующим формулам:
определяются по следующим формулам:
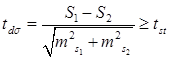
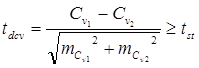
Критерий достоверности сравнивают со стандартным значением при числе степеней свободы: k=n1+n2-2
Рассмотрим статистические ошибки для коэффициента корреляции r при большом и малом числе наблюдений и достоверность разницы между двумя r.
При большом числе наблюдений (n≥100) и при высоком значении коэффициента корреляции ошибку вычисляют по следующей формуле:
или
где r — коэффициент корреляции, вычисленной при n>100; n—число наблюдений в выборке.
При малых выборках (n<100) формула ошибки коэффициента корреляции принимает следующий вид:

Критерий достоверности 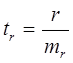 может быть заменен следующим выражением:
может быть заменен следующим выражением: 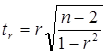 , что значительно упрощает вычисление.
, что значительно упрощает вычисление.
Для определения достоверности r при данном вычисленном значении t в условиях, когда n<100, пользуются достоверными значениями t 0,95 ;t 0,99 ;
t 0,999, получаемыми из таблицы (см. приложение 1) с учётом числа степеней свободы k. Для t r число степеней свободы определяется по формуле: k=n-2
Если вычисление 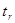 будет больше табличных значений t, то коэффициент корреляции r достоверен, т.е. правильно отражает связь данных признаков в генеральной совокупности.
будет больше табличных значений t, то коэффициент корреляции r достоверен, т.е. правильно отражает связь данных признаков в генеральной совокупности.
Если вычисленное t<tst –выборочный коэффициент корреляции недостоверен, что не даёт возможности сделать какое-либо заключение о связи признаков в генеральной совокупности.
Достоверность разности коэффициентов корреляции определяется так же, как и достоверность разности средних, по обычной формуле:
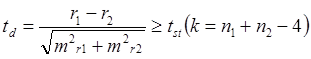
Ошибка коэффициента регрессии равна ошибке коэффициента корреляции, умноженной на соотношение σ:
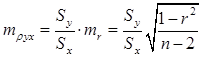
Если требуется исчислить ошибку для коэффициента регрессии 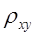 , то:
, то:
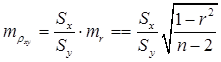
Критерий достоверности:
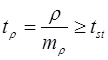
Стандартное значение критерия  определяют при числе степеней свободы k=n-2
определяют при числе степеней свободы k=n-2
Критерий достоверности разности двух коэффициентов регрессии.
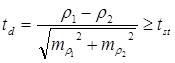
Число степеней свободы k=n1+n2-4
Дата добавления: 2016-04-11; просмотров: 5089;
