Однофакторный дисперсионный анализ.
Предположим, что имеется 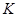 выборок с объемами
выборок с объемами  ,
, 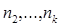 ,
, 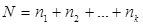 , и наблюдения можно представить в виде
, и наблюдения можно представить в виде 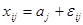 , где
, где 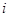 - номер наблюдения в выборке;
- номер наблюдения в выборке; 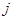 - номер выборки;
- номер выборки; 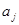 - групповые математические ожидания;
- групповые математические ожидания; 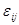 - случайные ошибки с
- случайные ошибки с  =0, о которых предполагается, что они независимы и одинаково расположены.
=0, о которых предполагается, что они независимы и одинаково расположены.
Подобная ситуация возникает, когда существует некий фактор, принимающий 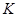 различных значений (называемых уровнями), и каждая группа объектов, чьи признаки мы примеряем, подвергается воздействию определенного уровня этого фактора. Методы математической статистики, изучающие воздействие одного фактора на объекты и их признаки, называют в совокупности однофакторным анализом.
различных значений (называемых уровнями), и каждая группа объектов, чьи признаки мы примеряем, подвергается воздействию определенного уровня этого фактора. Методы математической статистики, изучающие воздействие одного фактора на объекты и их признаки, называют в совокупности однофакторным анализом.
Предполагается, что ошибки нормально распределены:  . Тогда можно изучать влияние фактора, вычисляя дисперсии некоторых величин. Совокупность этих методов называют однофакторным дисперсионным анализом.
. Тогда можно изучать влияние фактора, вычисляя дисперсии некоторых величин. Совокупность этих методов называют однофакторным дисперсионным анализом.
Основной гипотезой, нуждающейся в проверке, является гипотеза о равенстве групповых средних 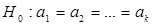 . Иными словами, проверяют гипотезу о том, что фактор вообще не влияет на наблюдения. В случае нормальных ошибок ее можно проверить, вычислив две разные оценки дисперсии.
. Иными словами, проверяют гипотезу о том, что фактор вообще не влияет на наблюдения. В случае нормальных ошибок ее можно проверить, вычислив две разные оценки дисперсии.
Рассмотрим группу экспериментальных животных, подвергнутых ультрафиолетовому облучению. В процессе эксперимента измерялась температура тела животных. Результаты измерений были занесены в таблицу:
| № испытания | Уровень фактора А (мощность ультрафиолетового облучения) | ||
| А1 | А2 | А3 | |
| 37,4 37,3 37,0 36,9 | 37,8 37,9 37,5 37,4 | 38,0 37,9 38,4 38,3 | |
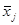
| 37,15 | 37,65 | 38,15 |
Физический фактор А (ультрафиолетовое излучение) имеет 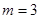 постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными.
постоянных уровней (3 различных мощности облучения). На всех уровнях распределения случайной величины Х (температуры тела животного) предполагается нормальным, а дисперсии одинаковыми, хотя и неизвестными.
В данном эксперименте число проведенных наблюдений при действии каждого из уровней фактора одинаково.
Все значения величины Х, наблюдаемые при каждом фиксированном уровне фактора Аj, составляют группу, и в последней строке таблицы представлены соответствующие выборочные групповые средние, вычисленные по формуле
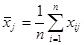 .
.
Здесь n – число испытаний, 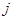 – номер столбца,
– номер столбца, 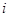 - номер строки, в которой расположено данное значение случайной величины. Общая средняя арифметическая всех
- номер строки, в которой расположено данное значение случайной величины. Общая средняя арифметическая всех 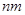 наблюдений находится как
наблюдений находится как
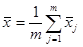 .
.
Введем следующие понятия:
Факторная сумма квадратов отклонений групповых средних от общей средней 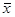 , которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):
, которая характеризует рассеивание «между группами» (т.е. рассеивание за счет исследуемого фактора):
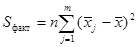 ,
,
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней 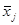 , которая характеризует рассеивание «внутри групп» (за счет случайных причин):
, которая характеризует рассеивание «внутри групп» (за счет случайных причин):

 .
.
Общая сумма квадратов отклонений наблюдаемых значений от общей средней 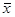 :
:
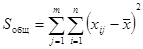 ,
,
Можно доказать следующее равенство:

 .
.
С помощью 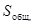 ,
, 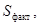
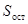 производится оценка общей, факторной и остаточной дисперсий:
производится оценка общей, факторной и остаточной дисперсий:
 ,
,
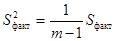 ,
,
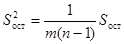 .
.
В основе однофакторного дисперсионного анализа лежит тесная связь между различием в групповых средних 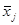 и соотношением между двумя видами дисперсий – факторной, которая характеризует влияние фактора А на величину Х, и остаточной, которая характеризует влияние случайных причин. Сравнивая факторную дисперсию с остаточной по величине их отношения судят, насколько сильно проявляется влияние фактора.
и соотношением между двумя видами дисперсий – факторной, которая характеризует влияние фактора А на величину Х, и остаточной, которая характеризует влияние случайных причин. Сравнивая факторную дисперсию с остаточной по величине их отношения судят, насколько сильно проявляется влияние фактора.
Для сравнения двух дисперсий используют показатель критерия Фишера 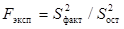 .
.
При этом при заданном уровне значимости проверяют нулевую гипотезу о равенстве факторной и остаточной дисперсии (изучаемый фактор не вызывает изменчивости признака) при конкурирующей гипотезе об их неравенстве (изучаемый фактор вызывает изменчивость признака).
По таблице критических значений распределения Фишера – Снедекора (см. приложение 6) при уровне значимости, равном половине заданного уровня 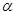 , находят критическое значение
, находят критическое значение 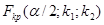 . Здесь
. Здесь 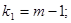
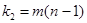 . Если
. Если 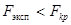 , нулевую гипотезу считают согласующейся с результатами наблюдений. Если
, нулевую гипотезу считают согласующейся с результатами наблюдений. Если 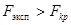 , то эту гипотезу отвергают в пользу конкурирующей.
, то эту гипотезу отвергают в пользу конкурирующей.
Замечание. Если окажется, что  , следует сделать вывод об отсутствии влияния фактора А на Х.
, следует сделать вывод об отсутствии влияния фактора А на Х.
Если проверка покажет значимость различий между 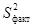 и
и 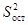 ,следует сделать вывод о существенном влиянии фактора А на Х.
,следует сделать вывод о существенном влиянии фактора А на Х.
Обычно для упрощенная расчетов фактурную и остаточную дисперсии рассчитывают не по экспериментальным значениям  величины Х, а по значениям
величины Х, а по значениям 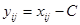 , где постоянная С представляет собой произвольное число, близкое к среднему значению
, где постоянная С представляет собой произвольное число, близкое к среднему значению 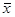 всех результатов наблюдений.
всех результатов наблюдений.
Вернемся к нашему примеру. Вычтем из всех значений  постоянное число С=37,5 близкое к общему среднему
постоянное число С=37,5 близкое к общему среднему 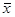 =37,51 и составим таблицу:
=37,51 и составим таблицу:
 Общая средняя будет равна
Общая средняя будет равна 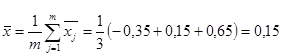
Определим значения 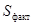 ,
, 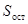
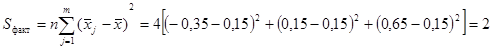
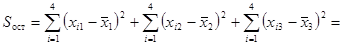


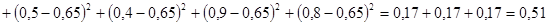
Определим значения факторной и остаточной дисперсий:
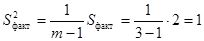 ,
,
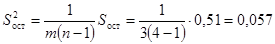 .
.
Так как  , следует проверить значимость их различия. Найдем экспериментальное значение критерия:
, следует проверить значимость их различия. Найдем экспериментальное значение критерия:
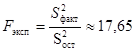 .
.
Сравним его с критическим значением распределения Фишера – Снедекора для уровня значимости 0,05 (см. приложение 6):
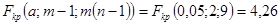 .
.
Поскольку 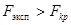 можно утверждать, что при уровне значимости
можно утверждать, что при уровне значимости
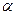 =0,05 рассматриваемый физический фактор оказывает влияние на температуру тела животного.
=0,05 рассматриваемый физический фактор оказывает влияние на температуру тела животного.
Критерий Фишера указывает на влияние изучаемого фактора (если 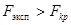 ) на изменчивость признака. Однако он не указывает на силу влияния этого фактора. В качестве показателя силы влияния фактора на изменчивость признака используют величину
) на изменчивость признака. Однако он не указывает на силу влияния этого фактора. В качестве показателя силы влияния фактора на изменчивость признака используют величину 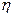 :
:
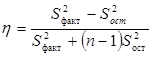 .
.
Оценим силу влияния ультрафиолетового облучения на повышение температуры тела животных:
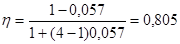
 или 80,5%
или 80,5%
Таким образом, влияние ультрафиолетового облучения на повышение температуры тела животных составляет 80,5%, а 19,5% обусловлены случайными причинами.
Дата добавления: 2016-04-11; просмотров: 983;
