Структура сети Петри

Сеть Петри состоит из четырех элементов: множество позиций Р, множество переходов Т, входная функция I и выходная функция O. Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход t_j в множество позиций I(t_j), называемых входными позициями перехода. Выходная функция O отображает переход t_j в множество позиций O (t_j), называемых выходными позициями перехода.

Структура сети Петри определяется ее позициями, переходами, входной и выходкой функциями.

Определение 1.1. Сеть Петри С является четверкой, С = {Р, Т, I, О). Р = {p₁, p₂, …, p_n} – конечное множество позиций, n ≥ 0. Т = {t₁, t₂, …, t_m}–конечное множество переходов, m ≥ 0. Множество позиций и множество переходов не пересекаются, P ∩ T = Ø. I : T → P^∞ является входной функцией – отображением из переходов в комплекты позиций. O : T → P^∞ есть выходная функция – отображение из переходов в комплекты позиций.

Мощность множества Р есть число n, а мощность множества T есть число m. Произвольный элемент Р обозначается символом p_i, i = 1, …, n, а произвольный элемент Т – символом t_j, j = 1, …, m.

Примеры сетей Петри даны на рис. 1.1–1.4.

Позиция p_i является входной позицией перехода t_j в том случае, если p_i 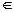I(t_j); p_i является выходной позицией, если p_i 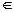O(t_j). Входы и выходы переходов представляют собой комплекты позиций. Комплект является обобщением множества, в которое включены многократно повторяющиеся элементы – тиражировании элементы. Использование комплектов, а не множеств для входов и выходов перехода позволяет позиции быть кратным входом либо кратным выходом перехода. Кратность входной позиции p_i для перехода t_j есть число появлений позиции во входном комплекте перехода, #( p_i, I(t_j)). Аналогично кратность выходной позиции p_i для перехода t_j есть число появлений позиции в выходном комплекте перехода, #( p_i, O(t_j)). Если входная и выходная функции являются множествами (а не комплектами), то кратность каждой позиции есть либо 0, либо 1.

Входные и выходные функции используются для отображений позиций в комплекты переходов, а также их можно использовать для отображения переходов в комплекты позиций. Определим, что переход t_j является входом позиции p_i , если p_i есть выход t_j. Переход t_j есть выход позиции p_i, если p_i есть вход t_j.

Определение 1.2. Определим расширенную входную функцию I и выходную функцию O I : P → T ^∞ , O : P → T ^∞ таким образом, что

#( t_j, I (p_i)) = #( p_i, O(t_j)), #( t_j, O(p_i)) = #( p_i, I (t_j)).

Для сети Петри на рис. 1.1 расширенными входной и выходной функциями являются:

С=(Р, Т, I, О),

P = {p₁, p₂, p₃, p₄},

T = {t₁, t₂, t₃, t₄, t₅, t₆},

I(p₁) = {} O(p₁) = {t₁}

I(p₂) = {t₁, t₄} O(p₂) = {t₂}

I(p₃) = {t₁, t₄} O(p₃) = {t₂, t₃}

I(p₄) = {t₃} O(p₄) = {t₄}

I(p₅) = {t₁, t₂} O(p₅) = {t₂}

Графы сетей Петри

В значительной степени теоретическая работа по сетям Петри основана на формальном определении сетей Петри, изложенном выше. Тем не менее для иллюстрации понятий теории сетей Петри гораздо более удобно графическое представление сети Петри. Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф.

Структура сети Петри представляет собой совокупность позиций и переходов. В соответствии с этим граф сети Петри обладает двумя типами узлов. Кружок О является позицией, а планка | – переходом.

Ориентированные дуги (стрелки) соединяют позиции и переходы, при этом некоторые дуги направлены от позиций к переходам, другие – от переходов к позициям. Дуга, направленная от позиции p_i к переходу t_j, определяет позицию, которая является входом перехода. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выходная позиция указывается дугой от перехода к позиции. Кратные выходы также представлены кратными дугами.

Сеть Петри есть мультиграф, так как он допускает существование кратных дуг от одной вершины графа к другой. Следует добавить, что так как дуги являются направленными, то это ориентированный мультиграф. Мы знаем, что вершины графа можно разделить на два множества (позиции и переходы) таким образом, что каждая дуга будет направлена от элемента одного множества (позиций или переходов) к элементу другого множества (переходов или позиций); следовательно, такой граф является двудольным ориентированным мультиграфом. В дальнейшем для простоты будем называть его просто графом сети Петри.

Определение 1.3. Граф G сети Петри есть двудольный ориентированный мультиграф, G = (V, А), где V = {v₁, v₂, …,v_s} – множество вершин, а А = {a₁, a₂, …, a_r} – комплект направленных дуг, a_i = (v_j, v_k), где v_j, v_k 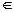V. 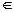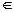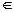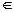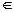Множество V может быть разбито на два непересекающихся подмножества Р и Т, таких, что V = Р U Т, Р ∩ Т = Ø, и для любой направленной дуги a_i А, если a_i = (v_j, v_k), тогда либо v_j, Р, v_k Т, либо v_j, Т, v_k Р.

Графы сети Петри, изображенные на рис. 1.5 – 1.8, эквивалентны соответственно структурам сети Петри на рис. 1.1 –1.4.

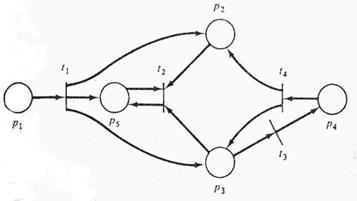
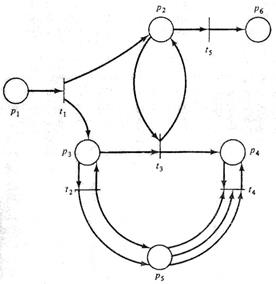
Рис. 1.5. Граф сети Петри на рис. 1.1. Рис. 1.6. Граф сети Петри на рис. 1.2

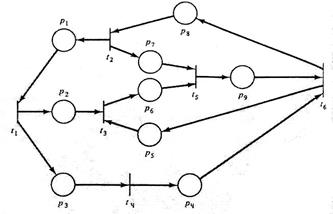
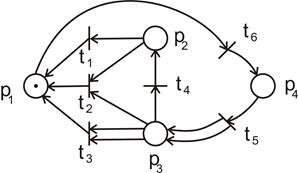
Рис. 1.7. Граф сети Петри на рис. 1.3. Рис. 1.8. Граф сети Петри на рис. 1.4

Для демонстрации эквивалентности этих двух представлений сети Петри – структуры сети Петри и графа сети Петри – покажем, каким образом можно преобразовать один в другой. Предположим, нам дана структура сети Петри С = {Р, Т, I, О) с Р = {p₁, p₂, …, p_n},. Т = {t₁, t₂, …, t_m}. Тогда граф сети Петри можно определить следующим образом.

Определение 1.4. Определим V = P U T. Определим А как комплект направленных дуг, такой, что для всех p_i 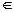Р и t_j 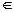Т

#((p_i ,t_j), А) = #( p_i, I(t_j)), #( t_j, p_i), А) = #( p_i, O(t_j)).

G = (V, А) – граф сети Петри, эквивалентный структуре сети Петри С = (Р, Т, I, О).

Обратное преобразование (от графа сети Петри к структуре) осуществляется подобным образом. Однако при переходе от графа сети Петри к структуре сета Петри возникает одна интересная задача: если множество вершин можно разделить на подмножества S и R, то какое из этих подмножеств должно бьет позициями, а какое — переходами? Оба возможных варианта позволяют определить сеть Петри, хотя в получающихся в результате структурах позиции и переходы меняются местами.

Двойственной к сети Петри С = (Р, Т, I, О) является сеть Петри 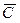= (Т, Р, I, О), которая получается в результате перестановки позиций и переходов. Структура графа сохраняется, просто меняются местами кружки и планки. На рис. 1.9, 1.10 показаны сети, двойственные к сетям Петри на рис. 1.5 и рис. 1.8.

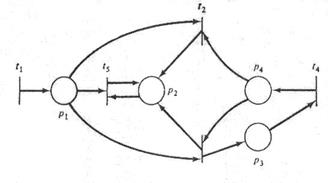
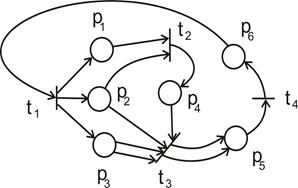
Рис. 1.9. СП, двойственная к СП на рис. 1.5 Рис. 1.10. СП, двойственная к СП на рис. 1.8

Инверсная сеть Петри – С для сети Петри С = (Р, Т, I, О), определяется! перестановкой входной и выходной функций – С = (Р, Т, О, I). То есть граф для сети Петри, инверсной сети Петри на рис. 1.8. будет выглядеть как на рис.1.11.

Графы сети Петри являются мультиграфами, так как позиция может быть кратным входом или выходом перехода. В графе это показывается несколькими дугами между позицией и переходом. В то время как такой способ удовлетворителен для дуг с малой кратностью (не более трех), он неудобен для дуг очень большой кратности. Таким образом, в качестве альтернативного представления структур с большой краткостью используется пучок дуг. Пучок – это специальная дуга, которая рисуется жирной линией и помечается кратностью. Рис. 1.12 иллюстрирует переход с входной кратностью 7 и выходной кратностью 11.

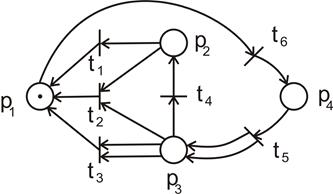
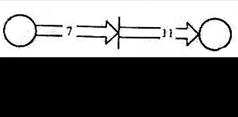
Рис. 1.11. СП, инверсная к СП на рис. 1.8 Рис. 1.12. Пучок дуг