Маркировка сетей Петри

Маркировка μ, есть присвоение фишек позициям сети Петри. Фишка – это примитивное понятие сетей Петри (подобно позициям и переходам). Фишки присваиваются (можно считать, что они принадлежат) позициям. Количество и положение фишек при выполнении сети Петри могут изменяться. Фишки используются для определения выполнения сети Петри.

Определение 1.5. Маркировка μ сети Петри С = (Р, Т, I, О) есть функция, отображающая множество позиций Р в множество неотрицательных целых чисел N.

μ : Р → N.

Маркировка μ, может быть также определена как n-вектор μ = (μ₁, μ₂, …, μ_n), где n = |P| и каждое μ _i 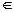N, i = 1, …, n. Вектор μ определяет для каждой позиции p_i сети Петри количество фишек в этой позиции. Количество фишек в позиции p_i есть μ _i , i = 1, …, n. Связь между определениями маркировки как функции и как вектора очевидным образом устанавливается соотношением
μ(p_i) = p_i . Обозначение ее в виде функции является несколько более общим и поэтому употребляется гораздо чаще.

Маркированная сеть Петри M = (C, μ) есть совокупность структуры сети Петри С = (Р, Т, I, О) и маркировки μ и может быть записана в виде
M = (Р, Т, I, О, μ).

На графе сети Петри фишки изображаются маленькой точкой в кружке, который представляет позицию сети Петри. На рис 1.13 приведен пример графического представления маркированной сети Петри.

Так как количество фишек, которое может быть определено для каждой позиции, неограниченно, то в целом для сети Петри существует бесконечно много маркировок. Множество всех маркировок сети Петри, обладающей n позициями, есть множество всех n-векторов, Nⁿ. Это множество, хотя и бесконечно, является счетным.

Количество фишек в сети Петри редко превышает 5 или 6. В этом случае их рисуют. Однако, когда маркировка имеет 10, 20 или сотни фишек, приписанных позиции, в кружках удобнее не рисовать фишки, а указывать их общее количество, как на рис. 1.14.

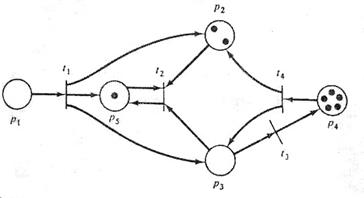
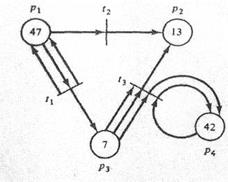
Рис. 1.13. Маркированная сеть Петри Рис. 1.14. Сеть Петри с большой маркировкой