Пространство состояний сети Петри

Состояние сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети Петри посредством изменения маркировки сети. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т.е. N ⁿ. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения δ, которую мы назовем функцией следующего состояния. Когда эта функция применяется к маркировке μ (состоянию) и переходу t_j, она образует новую маркировку (состояние), которая получается при запуске перехода t_j в маркировке μ. Так как t_j может быть запущен только в том случае, когда он разрешен, то функция δ(μ, t_j) не определена, если t_j не разрешен в маркировке μ. Если же t_j разрешен, то δ(μ, t_j) = μ', где μ' есть маркировка, полученная в результате удаления фишек из входов t_j и добавлением фишек в выходы t_j.

Определение 1.8. Функция следующего состояния δ : N ⁿ 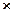Т → N ⁿ для сети Петри С = (Р, Т, I, О) с маркировкой μ и. и переходом t_j 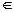Т определена тогда и только тогда, когда μ ( p_i ) ≥ #( p_i, I(t_j)) . для всех p_i 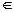P. Если
δ(μ, t_j) определена, то δ(μ, t_j) = μ', где для μ'( p_i ) = μ( p_i ) – #( p_i, I(t_j)) + #( p_i, O(t_j)). для всех p_i 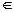P.

Пусть дана сеть Петри С = (Р, Т, I, О) с начальной маркировкой μ⁰. Эта сеть может быть выполнена последовательными запусков переходов. Запуск разрешенного перехода t_j в начальной маркировке образует новую маркировку μ¹ = δ(μ⁰, t_j). В этой новой маркировке можно запустить любой другой разрешенный переход, например t_k, образующий новую маркировку μ² = δ(μ¹, t_k). Этот процесс будет продолжаться до тех пор, пока в маркировке будет существовать хотя бы один разрешенный переход. Если же получена маркировка, в которой ни один переход не разрешен, то никакой переход не может быть запущен, функция следующего состояния не определена для всех переходов, и выполнение сети должно быть закончено.

При выполнении сети Петри получаются две последовательности: последовательность маркировок (μ⁰, μ¹, μ², ...) и последовательность переходов., которые были запущены (t_j0, t_j1, t_j2, ...). Эти две последовательности связаны следующим соотношением: δ(μ^k, t_jk) = μ^k+1 для k = 0, 1, 2, ... . Имея последовательность переходов и μ⁰ легко получить последовательность маркировок сети Петри, а имея последовательность маркировок, легко получить последовательность переходов, за исключением нескольких вырожденных случаев. Таким образом, обе эти последовательности представляют описание выполнения сети Петри.

Пусть некоторый переход в маркировке μ разрешен и, следовательно, может быть запущен. Результат запуска перехода в маркировке μ есть новая маркировка μ'. Говорят, что μ' является непосредственно достижимой из маркировки μ, иными словами, состояние μ' непосредственно получается из состояния μ.

Определение 1.9. Для сети Петри С = (Р, Т, I, О) с маркировкой μ маркировка μ' называется непосредственно достижимой из μ, если существует переход t_j 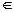Т, такой, что δ(μ, t_j) = μ'.

Можно распространить это понятие на определение множества достижимых маркировок данной маркированной сети Петри. Если μ' непосредственно достижима из μ, a μ" – из μ', говорят, что μ" достижима из μ. Определим множество достижимости R(С, μ) сети Петри С с маркировкой μ как множество всех маркировок, достижимых из μ. Маркировка μ' принадлежит R(C, μ), если существует какая-либо последовательность запусков-переходов, изменяющих μ на μ'.

Определение 1.10. Множество достижимости R(C, μ) для сети Петри С = (Р, Т, I, О) ) с маркировкой μ есть наименьшее множество маркировок, определенных следующим образом:

1. μ 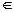R(C, μ);

2. Если μ' 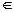R(C, μ) и μ" = δ(μ', t_j) для некоторого t_j 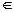Т, то μ" 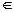R(C, μ).

Для сети Петри, изображенной на рис. 1.17, и маркировки μ = (1, 0, 0) непосредственно достижимыми являются две маркировки: (0, 1, 0) и (1, 0, 1). Из (0, 1, 0) нельзя достичь ни одной маркировки, так как ни один переход не разрешен. Из (1, 0, 1) можно получить (0, 1, 1) и (1, 0, 2). Далее мы покажем, что множество достижимости R(C, μ) имеет следующий вид: {(1, 0, n), (0, 1, n) | n ≥ 0}.

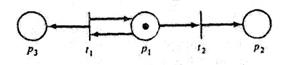
Рис. 1.17. Маркированная сеть Петри

Удобно распространить функцию следующего состояния на отображение маркировки и последовательности переходов в новую маркировку. Для последовательности переходов (t_j1, t_j2, …, t_jk) и маркировки μ маркировка μ' = δ(μ, t_j1, t_j2, …, t_jk) есть результат запусков: сначала – t_j1, затем – t_j2 и т.д. до t_jk. (Такая операция, конечно, возможна только в том случае, если каждый переход к моменту его запуска разрешен.)

Определение 1.11. Расширенная функция следующего состояния определяется для маркировки μ и последовательности переходов σ 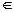Т* (где Т* – множество всех подмножеств множества (булеан) переходов) следующими соотношениями: δ(μ, t_j, σ) = δ(δ(μ, t_j), σ), δ(μ, λ) = μ. Обычно мы применяем эту расширенную функцию.

Упражнения

1. Найдите расширенную входную и выходную функции сетей Петри рис. 1.2 – 1.4.

2. Постройте графы сетей Петри, двойственные к сетям Петри, показанным на рис. 1.6 и 1.7.

3. Постройте граф сети Петри для следующей структуры сети Петри:

P = {p₁, p₂, p₃, p₄}, T = {t₁, t₂, t₃, t₄, t₅},

I(t₁) = { } O(t₁) = { p₁}

I(t₂) = {p₁} O(t₂) = { p₂}

I(t₃) = {p₂, p₄} O(t₃) = {p₁, p₃}

I(t₄) = { } O(t₄) = {p₃}

I(t₅) = {p₃} O(t₄) = {p₄}

4. Постройте граф сети Петри для следующей структуры сети Петри:

P = {p₁, p₂}, T = {t₁, t₂, t₃,},

I(t₁) = {p₁} O(t₁) = { p₁, p₂}

I(t₂) = {p₁} O(t₂) = { p₂}

I(t₃) = {p₂} O(t₃) = {}

5. Найдите структуру сети Петри, соответствующую графу сети Петри на рис. 1. 18. Определите структуру сети Петри для графа на рис. 1.19.

6. Найдите структуру инверсной сети Петри, соответствующую графу сети Петри на рис. 1.18 и графу на рис. 1.19.

7. Опишите мультиграфы сети Петри в виде G = (V, А), для графов сети Петри на рис. 1. 26 и рис. 1.27.

8. По сети Петри, заданной четверкой C = (P, T, I, O) (упражнение 3) построить двойственную ей сеть Петри в виде графа и четверки C = (P, T, I, O).

9. Найти расширенную входную и выходную функции сети Петри на рис. 1.19

10. Для сети Петри, заданной в виде графа (рис. 1.18) записать теоретико-формальное представление в виде четверки C = (P, T, I, O)

11. По графу сети Петри построить двойственную ей сеть Петри в виде графа и четверки C = (P, T, I, O).

12. По графу сети Петри (рис. 1.19) построить ее теоретико-формальное представление в виде четверки C = (P, T, I, O) и описать граф в виде G = (V, A).

13. Для маркированной сети Петри, граф которой изображен на рис. 1.20, представить маркировку как функцию и как n-вектор.

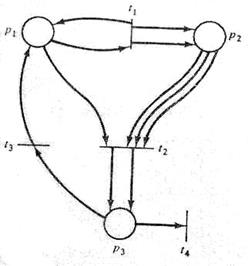
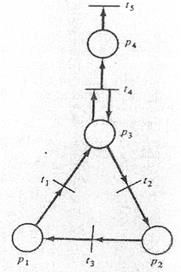
Рис. 1.18. Граф сети Петри Рис. 1.19. Граф сети Петри

14. Нарисуйте граф сети Петри для следующей структуры

P = {p₁, p₂, p₃, p₄}, T = {t₁, t₂, t₃, t₄},

I(t₁) = { } O(t₁) = { p₁, p₁, p₁, p₁, p₂}

I(t₂) = {p₂} O(t₂) = { p₁, p₁, p₁, p₁, p₁, p₁, p₃}

I(t₃) = {p₁, p₁, p₁, p₁, p₁, p₁} O(t₃) = {p₂, p₂, p₂, p₂, p₄, p₄}

I(t₄) = {p₃, p₄, p₄, p₂} O(t₄) = {}

15. Изобразите инверсную сеть Петри для сетей Петри, приведенных на рис. 1.12 и рис. 1.13.

16. Для маркированной сети Петри (рис. 1.15) представьте маркировку как функцию и как вектор.

17. Для структуры сети Петри (рис. 1.2) изобразите граф сети Петри и укажите на графе маркировку μ = (1, 0, 1, 1, 0, 0).

18. Изобразите маркировку μ = (137, 22, 2, 0, 14) для сети Петри на рис. 1.15.

19. Какие переходы разрешены в маркированной сети Петри на рис. 1.13, рис. 1.15, рис. 1.16?

20. Какая маркировка получится при запуске разрешенных переходов t_j в маркированной сети Петри на рис. 1.13, рис. 1.15, рис. 1.16?

21. Можно ли запустить переходы в сети Петри на рис. 1.20? Какие?

22. Определите последовательность маркировок для маркированной сети Петри (рис. 1.21) и последовательности переходов t₁, t₂, t₃, t₄, t₅ . Как выглядит соответствующая последовательность переходов для последовательности маркировок (1, 0, 0), (0, 0, 1), (0, 0, 0)?

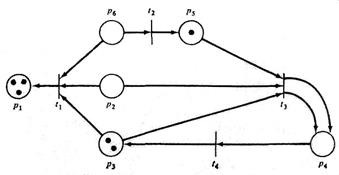
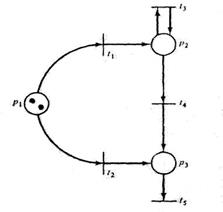
Рис. 1.20. Маркированная сеть Петри Рис. 1.21. Маркированная сеть Петри

23. Для маркированной сети Петри M = (P, T, I, O, µ) рис. 1.13 установить маркировку (1, 1, 1, 1, 1) и определить все функции следующего состояния δ(µ, t_j).

24. Определить последовательность маркировок µ⁰, µ¹, µ²... для последовательности переходов t₂, t₄, t₅, t₆, t₁, t₄ в сети Петри на рис. 1.15

25. Определить последовательность переходов t_j1, t_j2, t_j3… для заданной последовательности маркировок (0, 1, 0, 0) → (1, 1, 0, 0) → (2, 1, 0, 0) → (3, 1, 0, 0) → (3, 0, 1, 0) → (2, 0, 1, 0) → (1, 0, 1, 0) → (0, 0, 1, 0) в сети Петри рис. 3.5.

26. Определить возможные последовательности маркировок и переходов для сети Петри на рис. 1.21.

27. Определить все непосредственно достижимые маркировки для сети Петри на рис. 1.22:

28. Определить множество достижимости для сети Петри на рис. 1.23.

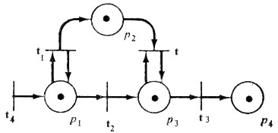
Рис. 1.22. Маркированная сеть Петри Рис. 1.21. Маркированная сеть Петри

29. Определить расширенную функцию следующего состояния δ(μ, t₁, t₁, t₁, t₁, t₂) для сети Петри на рис. 1.23.

30. Построить сеть Петри для перевода двоичного числа в десятичное.

31. Придумать игру на сети Петри, используя понятия фишек и правила запусков.