Тема 2. СЕТИ ПЕТРИ ДЛЯ МОДЕЛИРОВАНИЯ

События и условия

Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События – это действия, имеющие место в системе. Возникновением событий управляет состояние системы. Состояние системы может быть описано множеством условий. Условие – есть предикат или логическое описание состояния системы. Условие может принимать либо значение «истина», либо значение «ложь».

Так как события являются действиями, то они могут происходить. Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение предусловий и может привести к выполнению других условий – постусловий.

В качестве примера рассмотрим задачу моделирования простого автомата-продавца. Автомат-продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются: а) автомат-продавец ждет; б) заказ прибыл и ждет; в) автомат-продавец выполняет заказ; г) заказ выполнен. Событиями будут: 1. Заказ поступил. 2. Автомат-продавец начинает выполнение заказа. 3. Автомат-продавец заканчивает выполнение заказа. 4. Заказ посылается на доставку.

Предусловия события 2 (автомат-продавец начинает выполнение заказа) очевидны: (а) автомат-продавец ждет; (б) заказ прибыл и ждет. Постусловие для события 2: (в) автомат-продавец выполняет заказ. Аналогично мы можем определить предусловия и постусловия для других событий и составить следующую таблицу событий и их пред- и постусловий:

Такое представление системы легко моделировать сетью Петри. В сети Петри условия моделируются позициями, события – переходами. При этом входы перехода являются предусловиями соответствующего события; выходы – постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий.

Сеть Петри на рис. 2.1. иллюстрирует модель этого автомата-продавца. Мы указали каждому переходу и позиции соответствующие событие и условие.

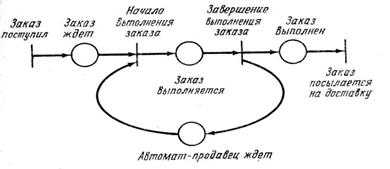
Рис. 2.1. Сеть Петри для простого автомата-продавца.

Можно моделировать и более сложную систему. Система автомат-продавец состоит из трех различных автоматов M1 , М2 и M3 и двух операторов F1 и F2. Оператор F1 воздействует на автоматы M1 и М2, а оператор F2 — на M1 и М3. Заказы требуют двух стадий обработки. Сначала они должны быть обработаны автоматом М1, затем либо автоматом М2, либо М3. Эта более сложная система будет иметь следующие условия:

а) заказ прибыл и ждет обработки автоматом M1;

б)заказ обработан автоматом M1 и ждет обработки либо автоматом М2, либо М3;

в) заказ выполнен;

г) автомат М1 незанят;

д) автомат М2 незанят;

е) автомат М3 незанят;

ж) оператор F1 незанят;

з) оператор F2 незанят;

и) автомат M1 находится под воздействием оператора F1,

к) автомат М1 находится под воздействием оператора F2;

л) автомат М2 находится под воздействием оператора F1;

м) автомат М3 находится под воздействием оператора F2.

При этом могут происходить следующие события:

1. Поступление заказа.

2. Оператор F1 начинает выполнение заказа на автомате М1.

3. Оператор F1 закончил выполнение заказа на автомате M1.

4. Оператор F2 начинает выполнение заказа на автомате M1.

5. Оператор F2 закончил выполнение заказа на автомате M1.

6. Оператор F1 начинает выполнение заказа на М2.

7. Оператор F1 закончил выполнение заказа на М2.

8. Оператор F2 начинает выполнение заказа на М3.

9. Оператор F2 закончил выполнение заказа на М3.

10. Заказ посылается на доставку.

Пред- и постусловия каждого события:

Сеть Петри этой системы показана на рис. 2.2.

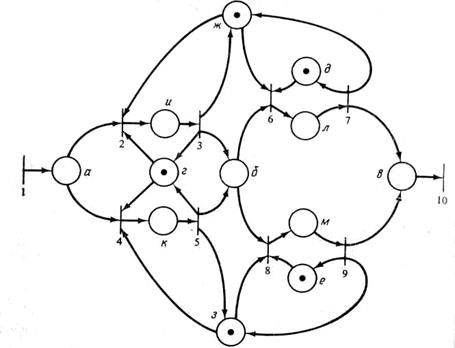
Рис. 2.2. Сеть Петри для сложного автомата-продавца

Упражнения

1. Построить сеть Петри «Деканат». Качественная постановка задачи: заявления поступают от студентов в приемную в неограниченном количестве. Далее заявление подписывается одним из двух заместителей декана, свободных в данный момент. После этого любой из свободных зам.декана, ставит печать, если она свободна. Далее заявление помещается в папку «к выдаче» и его можно забрать.

2. Построить сеть Петри «Деканат», описанную в задаче 1, считая, что заявление сначала получает печать, а затем расписывается один из зам. декана.

3. На примере сети Петри, построенной в задаче 1, указать переходы, находящиеся в конфликте, и ситуацию одновременности. Определить примитивные и непримитивные события, возникающие в системе.

4. Построить сеть Петри «Экзамен». Качественная постановка задачи: студент получает билет, решает задачу, отвечает устно, получает оценку. При невозможности решения или ответа имеет право на одну попытку взять второй билет.

Конечные автоматы

Аппаратное обеспечение ЭВМ можно рассматривать на нескольких уровнях, и сети Петри могут моделировать каждый из них. На низком уровне вычислительные системы могут быть описаны автоматами. Автомат – это пятерка (Q, Σ, Δ, δ, Г), где

Q – конечное множество состояний {q_l , q₂,.., q_k}\

Σ – конечный входной алфавит;

Δ – конечный выходной алфавит;

δ : Q 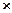Σ → Q – функция следующего состояния, отображающая текущее состояние и текущий вход в следующее состояние;

Г : Q 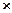Σ → Δ – функция выхода, отображающая текущее состояние и текущий вход в выходной символ.

Автоматы часто представляют в виде графов переходов, как, например, на рис. 2.3. В графе переходов состояния представляются кружками, являющимися вершинами. Дуга из состояния q_i в q_j , помеченная a/b, означает, что, находясь в состоянии q_i автомат при входе а перейдет в состояние q_j, выдавая при этом символ b. Формально следовало бы записать δ(q_i, а) = q_j и Г (q_i, а) = b.

Входной алфавит определяет входы автомата из внешнего мира, а выходной алфавит – выходы автомата во внешний мир.

В качестве примера рассмотрим автомат, изображенный на рис. 2.3. Этот автомат преобразует двоичное число, представленное последовательностью бит, начиная с младшего, в дополнение до двух. В данном случае входной и выходной алфавит состоит из трех символов: 0, 1 и R. Автомат начинает работать в состоянии q₁. Символ сброса (R) означает конец (или начало) числа и возвращает автомат в исходное состояние. Выход автомата для символа сброса является просто его повторением.

Аналогичный автомат показан на рис. 2.4. При тех же самых входах этот автомат вычисляет четность входного числа. Он начинает работу в состоянии q₁. Выход копирует вход до тех пор, пока входным символом не окажется символ сброса. Выходом для символа сброса будет 0 в случае нечетного числа и 1 – в случае четного числа.

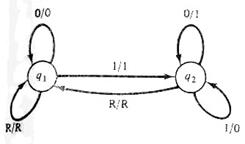
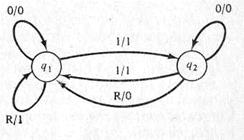
Рис. 2.3. Конечный автомат Рис. 2.4. Конечный автомат

При представлении конечного автомата сетью Петри следует обратить внимание на связь между сетью Петри и внешним миром, которая ранее не учитывалась. В нашей задаче мы моделируем это взаимодействие с помощью специального множества позиций. Позициями будут представлены каждый входной и выходной символы. Мы допускаем, что из внешнего мира помещается фишка в позицию, соответствующую входному символу, затем фишка, появившаяся в позиции, соответствующей выходному символу, удаляется оттуда.. Эта последовательность действий будет повторяться необходимое число раз. Задав представление позиций, соответствующих символам входа и выхода, мы можем завершить построение модели системы конечных состояний. Представим каждое состояние автомата позицией в сети Петри. Текущее состояние отмечается фишкой; все остальные позиции пусты. Теперь для определения переходов из состояния в состояние можно ввести переходы сети следующим образом. Для каждой пары (состояние и входной символ) мы определяем переход, входными позициями которого являются позиции, соответствующие состоянию и входному символу, а выходными позициями – позиции, соответствующие следующему состоянию и выходу.

Для конечного автомата (Q, Σ, Δ, δ, Г) мы определили сеть Петри
(Р, Т, I, О) таким образом:

P = Q U Σ U Δ , Т = {t_{q, σ} | q 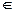Q, и 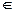σ Σ },

I(t_{q, σ}) = { q, σ }, О(t_{q, σ}) = { δ(q, σ), Г(q, σ)}.

Эта сеть Петри является моделью конечного автомата.

На рис. 2.6 изображена сеть Петри, соответствующая автомату с рис. 2.3, на рис. 2.7 – сеть Петри, соответствующая автомату с рис. 2.4.

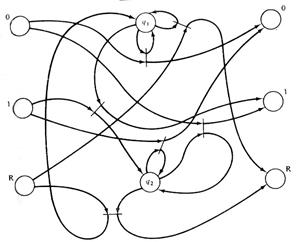
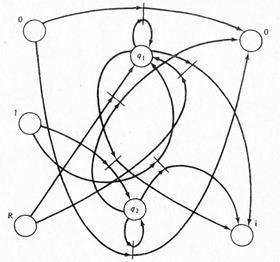
Рис. 2.6. СП, для автомата на рис. 2.3. Рис. 2.7. СП, для автомата на рис. 2.4.

Указание: для построения сети Петри по конечному автомату необходимо выполнить следующие действия:

а) построить конечный автомат ;

б) расписать пятерку (Q, Σ, Δ, δ, Г), определяющую конечный автомат ;

в) по пятерке (Q, Σ, Δ, δ, Г) получить теоретико-формальное описание сети Петри в виде четверки (Р, Т, I, О);

г) нарисовать граф сети Петри.

Упражнения

1. Построить конечный автомат и сеть Петри для проверки двоичного числа на четность.

2. Построить конечный автомат и сеть Петри для проверки правильности расстановки скобок (каждой открывающейся скобке соответствует закрывающаяся) в арифметическом выражении.

3. Построить конечный автомат и сеть Петри для проверки того, является ли последовательность символов идентификатором.

4. Построить конечный автомат и сеть Петри для проверки того, является ли последовательность символов арифметическим выражением.