Задачи анализа сетей Петри

Безопасность

Одно из важнейших свойств сети Петри, которая должна моделировать реальное устройство, – безопасность. Позиция сети Петри является безопасной, если число фишек в ней никогда не превышает 1. Сеть Петри безопасна, если безопасны все позиции сети.

Если позиция не является кратной входной или кратной выходной для перехода, ее можно сделать безопасной. К позиции p_i, которую необходимо сделать безопасной, добавляется новая позиция p'_i. Переходы, в которых p_i используется в качестве входной или выходной, модифицируются следующим образом:

Если p_i 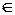I(t_j) и p_i 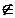О(t_j), тогда добавить p'_i к О(t_j).

Если p_i 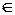О(t_j) и p_i 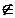I(t_j), тогда добавить p'_i к I(t_j).

Простая сеть Петри на рис. 4.1 преобразована в безопасную на рис. 4.2.

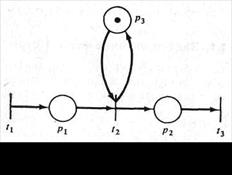
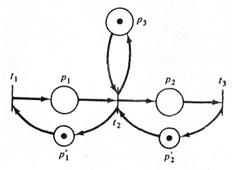
Рис. 3.1. Небезопасная сеть Петри. Рис. 3.2 Безопасная сеть Петри

Ограниченность

Безопасность – это частный случай более общего свойства ограниченности. Позиция является k-безопасной или k-ограниченной, если количество фишек в ней не может превышать целое число k.

1-безопасная позиция называется просто безопасной. Заметим, что граница k' по числу фишек, которые могут находиться в позиции, может быть функцией от позиции (например, позиция p₁ может быть 3-безопасной, тогда как позиция р₂ – 8-безопасной). Однако, если позиция p_i k -безопасна, то она также и k'-безопасна для всех k' ≥ k. Поскольку число позиций конечно, можно выбрать k, равное максимуму из границ каждой позиции, и определить сеть Петри k-безопасной, если каждая позиция сети k-безопасна.

Иногда нас будет интересовать только то, является число фишек в позиции ограниченным или нет, а не конкретное значение границы. Позиция называется ограниченной, если она k-безопасна для некоторого k; сеть Петри ограниченна, если все ее позиции ограниченны.

Сохранение

Определение 4.3. Сеть Петри С = (Р, Т, I, О) с начальной маркировкой μ называется строго сохраняющей, если для всех μ' 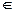R(C, μ )

.

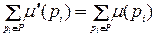Строгое сохранение – это очень сильное ограничение. Например, из него немедленно следует, что число входов в каждый переход должно равняться числу выходов, |I(t_j)| = |О(t_j)| . Если бы это было не так, запуск перехода изменил бы число фишек в сети.

Однако для более общего представления о свойстве сохранения рассмотрим рис. 4.3. Изображенная на нем сеть Петри не является строго сохраняющей, поскольку запуск перехода t₁ или t₂ уменьшит число фишек на 1, а запуск перехода t₃ или t₄ добавит фишку к маркировке. Мы можем тем не менее преобразовать эту сеть Петри в сеть на рис. 4.4, являющуюся строго сохраняющей.

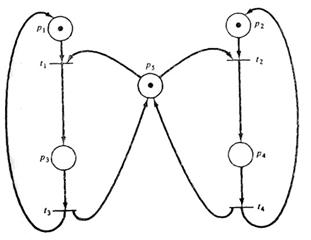
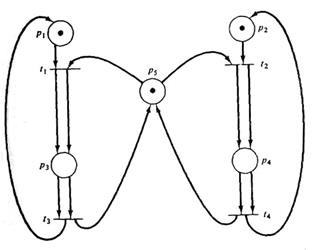
Рис. 3.3. Не строго сохраняющая сеть Петри Рис. 3.4. Строго сохраняющая сеть Петри

В общем можно определить взвешивание фишек. Взвешенная сумма для всех достижимых маркировок должна быть постоянной. Фишкам, не являющимся важными, можно присвоить вес 0; другим фишкам можно присвоить веса 1, 2, 3 или любое другое целое.

Фишка определяется ее позицией в сети, все фишки в позиции неразличимы. Следовательно, веса связываются с каждой позицией сети. Вектор взвешивания w = (w ₁, w ₂, ..., w _n) определяет вес w _i для каждой позиции p_i 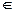P.

Сеть Петри С = (Р, Т, I, О) с начальной маркировкой μ называется сохраняющей по отношению к вектору взвешивания w, w = (w ₁, w ₂, ..., w _n), n = |Р|, w _i ≥ 0, если для всех μ' 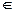R(C, μ )

.

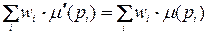Строго сохраняющая сеть Петри является сохраняющей по отношению к вектору взвешивания (1, 1, ..., 1). Все сети Петри являются сохраняющими по отношению к вектору взвешивания (0, 0, ..., 0). Поэтому сеть Петри будем называть сохраняющей, если она сохраняющая по отношению к некоторому положительному ненулевому вектору взвешивания w > 0 (с положительными ненулевыми весами, w_i > 0). Так сеть Петри с рис. 4.3 является поэтому сохраняющей, поскольку она сохраняющая по отношению к (1, 1, 2, 2, 1). Сеть Петри с рис. 3.4 не является сохраняющей.

Активность

Тупик в сети Петри – это переход (или множество переходов), которые не могут быть запущены. Переход называется активным, если он не заблокирован (нетупиковый). Это не означает, что переход разрешен, скорее он может быть разрешенным. Переход t_j сети Петри С называется потенциально запустимым в маркировке μ, если существует маркировка μ' 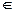R(C, μ), в которой t_j разрешен. Переход активен в маркировке μ, если потенциально запустим во всякой маркировке из R(C, μ). Следовательно, если переход активен, то всегда возможно перевести сети Петри из ее текущей маркировки в маркировку, в которой запуск перехода станет разрешенным.

Существуют другие, связанные с активностью понятия, которые рассматривались при изучении тупиков. Их можно разбить на категории по уровню активности и определить для сети Петри С с маркировкой μ следующим образом:

Уровень 0: Переход t_j обладает активностью уровня 0, если он никогда не может быть запущен.

Уровень 1: Переход t_j обладает активностью уровня 1, если он потенциально запустим, т.е. если существует такая t_j μ' 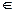R(C, μ), что t_j разрешен в μ'.

Уровень 2: Переход t_j обладает активностью уровня 2, если для всякого целого n существует последовательность запусков, в которой t_j присутствует по крайней мере n раз.

Уровень 3: Переход t_j обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой t_j присутствует неограниченно часто.

Уровень 4: Переход t_j обладает активностью уровня 4, если для всякой μ' 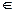R(C, μ) существует такая последовательность запусков σ, что t_j разрешен в δ(μ', σ).

Переход, обладающий активностью уровня 0, называется пассивным. Переход, обладающий активностью уровня 4, называется активным. Сеть Петри обладает активностью уровня i, если каждый ее переход обладает активностью уровня i.

В качестве примера, иллюстрирующего уровни активности, рассмотрим сеть Петри на рис. 3.5.

Переход t₀ не может быть запущен никогда; он пассивен. Переход t₁ можно запустить точно один раз; он обладает активностью уровня 1. Переход t₂ может быть запущен произвольное число раз, но это число зависит от числа запусков перехода t₃. Если мы хотим запустить t₂ пять раз, мы запускаем пять раз t₃, затем t₁ и после этого пять раз t₂. Однако, как только запустится t₁ (t₁ должен быть запущен до того, как будет как будет запущен t₂), число возможных запусков t₂ станет фиксированным. Следовательно, t₂ обладает активностью уровня 2, но не уровня 3. С другой стороны, переход t₃ можно запускать бесконечное число раз, и поэтому он обладает активностью уровня 3, но не уровня 4, поскольку, как только запустится t₁, t₃ больше запустить будет нельзя.