Дерево достижимости

Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 3.6. Начальная маркировка ее – (1, 0, 0). В этой начальной маркировке разрешены два перехода: t₁ и t₂. Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис. 3.7). Корневой (начальной) является вершина, соответствующая начальной маркировке. Это (частичное) дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.

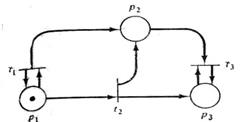
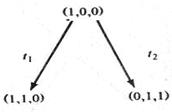
Рис. 3.6. Маркированная сеть Петри Рис. 3.7. Первый шаг построения дерева достижимости

Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1, 1,0) можно снова запустить t₁ ( получая (1, 2, 0)) и t₂ (получая (0, 2, 1)); из (0, 1, 1) можно запустить t₃ (получая (0, 0, 1)). Это порождает дерево, изображенное на рис. 3.8. Начиная с трех новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево, как показано на рис. 3.9. Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешенным, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут. Кроме того, необходимо отметить, что маркировка (0, 1, 1), порождаемая запуском t₃ в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском t₂.

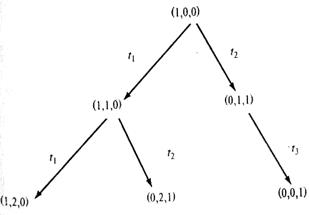
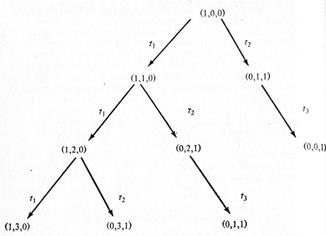
Рис. 3.8. Второй шаг построения дерева Рис. 3.9. Третий шаг построения дерева

Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порожденной. Однако получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рис. 3.10). Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера. (Заметим, что если какое-то представление бесконечного множества конечно, то бесконечное множество маркировок должно отображаться в такое представление. В общем случае это приведет к потере информации и, возможно, к тому, что некоторые свойств сетей Петри определить будет нельзя, но все зависит от того, как представление было получено.)

Приведение к конечному представлению осуществляется несколькими способами. Нам необходимо найти те средства, которые ограничивают введение новых маркировок (называемых граничными вершинами) на каждом шаге. Здесь могут помочь пассивные маркировки – маркировки, в которых нет разрешенных переходов. Эти пассивные маркировки называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Такие дублирующие маркировки называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве. Таким образом, в дереве на рис. 3.9 маркировка (0, 1, 1), получившаяся в результате выполнения последовательности t₁t₂t₃, не будет порождать какие-либо новые вершины в дереве, поскольку она ранее встречалась в дереве в результате выполнения последовательности t₂ из начальной маркировки.

Для сведения дерева достижимости к конечному представлению используется еще одно средство. Рассмотрим последовательность запусков переходов σ, начинающуюся в начальной маркировке μ и кончающуюся в маркировке μ', μ' > μ. Маркировка μ' совпадает с маркировкой μ, за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях, т. е. μ' = μ + (μ' – μ) > 0. Теперь, поскольку на запуски переходов лишние фишки не влияют, последовательность σ можно запустить снова, начиная в μ', приходя к маркировке μ". Так как действие последовательности переходов σ добавило μ' – μ фишек к маркировке μ, она добавит также μ' – μ фишек и к маркировке μ', поэтому μ'' = μ' + (μ' – μ) или μ'' = μ + 2(μ' – μ). В общем можно запустить последовательность σ n раз, получив в результате маркировку μ + n(μ' – μ). Следовательно, для тех позиций, которые увеличивают число фишек последовательностью σ, можно создать произвольно большое число фишек, просто повторяя последовательность σ столько, сколько это нужно. В сети Петри на рис. 4.7, например, можно запустить переход t₁ столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в р₂.

Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим

ω + а = ω, а < ω , ω – а = ω, ω ≤ ω .

Для построения дерева достижимости необходимы только эти операции над ω.

Теперь можно точно сформулировать действительный алгоритм построения дерева достижимости. Каждая вершина i дерева связывается с расширенной маркировкой μ [i]; в расширенноq маркировке число фишек в позиции может быть либо неотрицательным целым, либо ω. Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые еще не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.

Алгоритм начинает с определения начальной маркировки корнем дерева, т.е. граничной вершиной. До тех пор пока имеются граничные вершины, они обрабатываются алгоритмом.

Пусть х – граничная вершина, которую необходимо обработать.

1. Если в дереве имеется другая вершина у, не являющаяся граничной, и с ней связана та же маркировка, μ[х] = μ[у]; то вершина х – дублирующая.

2. Если для маркировки μ[х] ни один из переходов не разрешен (т.е.
δ(μ[х], t_j) не определено для всех t_j 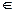Т), то х – терминальная вершина.

3. Для всякого перехода t_j 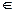Т, разрешенного в μ[х] (т.е. δ(μ[х], t_j) определено), создать новую вершину z дерева достижимости. Маркировка μ[z], связанная с этой вершиной, определяется для каждой позиции р_i следующим образом:

а) Если μ[х] _i = ω, μ[z] _i = ω.

б) Если на пути от корневой вершины к х существует вершина y с
μ[y] < δ(μ[х], t_j) и μ[y] _i < δ(μ[х], t_j) _i., то μ[z] _i = ω.

в) В противном случае μ [z] _i = δ(μ[х], t_j)_i.

Дуга, помеченная t_j, направлена от вершины х к вершине z. Вершина х переопределяется как внутренняя, вершина z становится граничной.

Когда все вершины дерева – терминальные, дублирующие или внутренние, алгоритм останавливается. На рис. 3.10 представлено дерево достижимости для сети Петри на рис. 4.6.

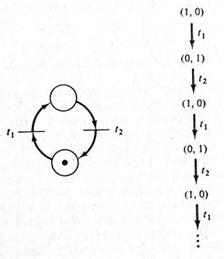
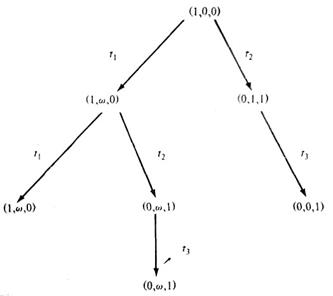
Рис. 3.9. Сеть Петри с бесконечным деревом Рис. 3.10. Конечное дерево достижимости

Дерево достижимости сети Петри с рис. 3.11 изображено на рис. 3.12.

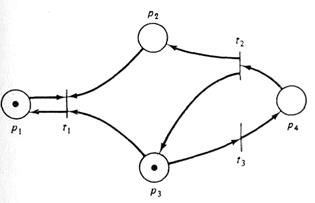
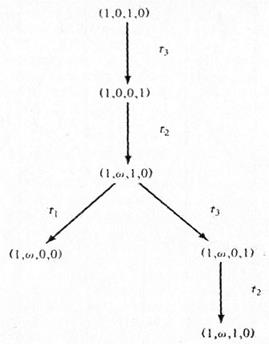
Рис. 3.11. Сеть Петри Рис. 3.12. Дерево достижимости сети Петри

Посмотрим, как можно использовать дерево достижимости для решения некоторых задач анализа сетей Петри.

Безопасность и ограниченность

Сеть Петри безопасна, если число фишек в каждой позиции не может превысить 1; сеть Петри ограниченна, если существует такое целое k, что число фишек в любой позиции не может превысить k. Оба этих свойства можно проверить с помощью дерева достижимости. Сеть Петри ограниченна тогда и только тогда, когда символ ω отсутствует в ее дереве достижимости. Присутствие символа ω в дереве достижимости означает, что число фишек потенциально не ограничено; существует последовательность запусков переходов, которую можно повторить произвольное число раз, увеличивая количество фишек до произвольно большого числа. Таким образом, если имеется символ ω, сеть неограниченна. Кроме того, положение символа ω показывает, какие позиции неограниченны.

Обратное утверждение также является верным, если сеть Петри неограниченна, то число достижимых маркировок бесконечно. Поскольку дерево достижимости конечно, бесконечное число достижимых маркировок отражает присутствие символа ω. Если сеть Петри ограниченна и символ ω отсутствует в дереве достижимости, то сеть Петри представляет систему конечных состояний. Дерево достижимости, по существу, является графом состояний и будет содержать вершину, соответствующую всякой достижимой маркировке. Это позволяет решить вопросы анализа простым перебором и проверкой конечного множества всех достижимых маркировок. Например, чтобы определить границу для заданной позиции, нужно построить дерево достижимости и найти наибольшее значение компоненты маркировки, соответствующей этой позиции.

Найденное значение является границей числа фишек для заданной позиции. Если граница для всех позиций не превышает 1, сеть безопасна.

На рис. 3.13 демонстрируется использование дерева достижимости для определения ограниченности.

Сохранение

Сеть Петри является сохраняющей, если она не теряет и не порождает фишки, а просто передвигает их. Поскольку две фишки можно закодировать как одну фишку, которая позже вызовет запуск перехода, создающего две фишки, значение фишки в каждой позиции определяет вектор взвешивания, веса неотрицательны Сеть Петри является сохраняющей по отношению к вектору взвешивания, если взвешенная сумма фишек постоянна для всех достижимых маркировок.

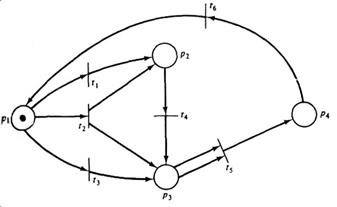
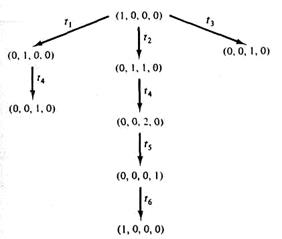
Рис. 3.13. Определение ограниченности для сети Петри с помощью дерева достижимости.

Свойство сохранения эффективно проверяется с помощью дерева достижимости. Так как дерево достижимости конечно, для каждой маркировки можно вычислить взвешенную сумму. Если сумма одинакова для каждой достижимой маркировки, сеть – сохраняющая по отношению к данному весу. Если суммы не равны сеть – несохраняющая.

При оценке сохранения необходимо быть внимательным с символом ω. Если маркировка имеет ω в качестве маркировки позиции p_i, тогда для того, чтобы сеть была сохраняющей, вес этой позиции должен быть равным 0. Напомним, что символ ω представляет бесконечное множество значений. Так как все веса неотрицательны, вес должен равняться либо нулю (тем самым означая, что число фишек в данной позиции не важно), либо быть положительным. Если вес положителен, то сумма будет разной для двух маркировок, различающихся в своей ω-компоненте. Следовательно, если какая-либо маркировка с ненулевым весом равна ω, сеть — несохраняющая.

Эти рассуждения относятся к сохранению по отношению к определенному взвешиванию. Сеть Петри является сохраняющей, если она сохраняющая по отношению к некоторому вектору w, w_i > 0. Дерево достижимости можно использовать для определения того, является сеть сохраняющей или нет, путем нахождения вектора весов w (если он существует). Заметим прежде всего, что для того, чтобы сеть Петри была сохраняющей по отношению к положительному вектору весов, она должна быть ограниченной. Как было указано выше, неограниченная позиция должна иметь нулевой вес, что недопустимо в сети с положительным вектором весов. (Если мы хотим допустить нулевые компоненты, нужно просто установить веса всех неограниченных позиций равными нулю и рассматривать после этого только оставшиеся компоненты.) Теперь, если сеть сохраняющая, существуют взвешенная сумма, обозначим ее s, и вектор весов
w = (w₁, w₂, ..., w_n). Для каждой маркировки μ[х] дерева достижимости имеем

w₁ · μ[х]₁ + w₂ · μ[х]₂ + ...+ w_n · μ[х]_n = s.

Это равенство определяет для k вершин дерева достижимости совокупность из k линейных уравнений с n + 1 неизвестными. Добавим к ним ограничения:
w_i > 0, i = 1, ..., n, в результате чего определим ограничения для вектора весов.

Решение этой системы линейных уравнений – хорошо известная задача, имеющая множество алгоритмов решения. Если ограничения, накладываемые на веса, являются чрезмерно жесткими и, следовательно, вектора взвешиваний не существует, это будет определено. В любом случае можно определить, является или нет сеть Петри сохраняющей, и если это так, получить вектор весов.

Покрываемость

Последняя задача, которую можно решить с помощью дерева, достижимости, – задача покрываемости. В задаче покрываемости мы хотим для данной маркировки μ' определить, достижима ли маркировка μ" ≥ μ'. Данная задача решается проверкой дерева достижимости. Строим для начальной маркировки μ дерево достижимости. Затем ищем любую вершину х с μ[х] ≥ μ'. Если такой вершины не существует, маркировка μ' не покрывается никакой достижимой маркировкой; если она найдена, μ[х] дает достижимую маркировку, покрывающую μ'.

Путь от корня к покрывающей маркировке определяет последовательность переходов, которые приводят из начальной маркировки к покрывающей маркировке, а маркировка, связанная с этой вершиной, определяет покрывающую маркировку. Символ ω вновь должен рассматриваться как обозначение бесконечного множества значений. Если компонента покрывающей маркировки – ω, то в пути от корня к покрывающей маркировке имеется «цикл». Для увеличения соответствующей компоненты с тем, чтобы она была не меньше, чем в данной маркировке, необходимо достаточное число раз повторить этот цикл.

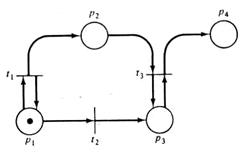
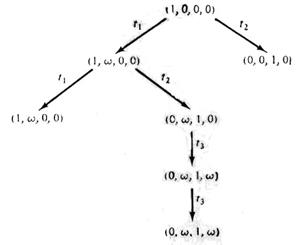
Рис. 3.14. Сеть Петри Рис. 3.15. Дерево достижимости сети Петри

Упражнения

1. Построить дерево достижимости для сети Петри С=(Р, Т, I, О), P = {p₁, p₂, p₃}, T = {t₁, t₂}, I(t₁) = {p₁, p₃}, I(t₂) = {p₂}, O(t₁) = {p₂}, O(t₂) = { p₁, p₃}

2. Построить дерево достижимости для сети Петри на рис. 3.5 и определить тип вершин.

3. Построить дерево достижимости и проверить на безопасность сети Петри с рис.2.14, рис.2.15, рис. 2.16.

4. Построить дерево достижимости и проверить, будет ли сеть Петри с рис.3.9 сохраняющей.

5. Построить дерево достижимости для сети Петри на рис. 3.5 и определить, будет ли покрываемы вершины (1, 1, 1, 0), (0, 1, 1, 0), (1, 1, 0, 0).

6. Построить дерево достижимости для сети Петри на рис. 3.5 и проверить, будет ли достижимы вершины (1, 3, 0, 0) и (0, 0, 1, 0).