Матричные уравнения

Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Альтернативным по отношению к определению сети Петри в виде (Р, Т, I, О) является определение двух матриц D ^– и D ⁺, представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим D ^– [j, i] = #(p_i, I(t_j)), a D ⁺ [j, i] = #(p_i, O(t_j)). D ^– определяет входы в переходы, D ⁺ – выходы.

Матричная форма определения сети Петри (Р, Т, D ^–, D ⁺) эквивалентна стандартной форме, используемой нами, но позволяет дать определения в терминах векторов и матриц. Пусть e[j] – m-вектор, содержащий нули везде, за исключением j-й компоненты. Переход t_j представляется m-вектором-строкой е[j].

Теперь переход t_j в маркировке μ разрешен, если μ ≥ e[j] · D ^–, а результат запуска перехода t_j в маркировке μ записывается как

δ(μ, t_j) = μ – e[j] · D ^– + e[j] · D⁺ = μ + e[j] · (– D ^– + D⁺ ) = μ + e[j] · D,

где D = D⁺ – D ^– – составная матрица изменений.

Тогда для последовательности запусков переходов σ = t_j1 t_j2 ... t_jk имеем

δ(μ, σ) = δ(μ, t_j1 t_j2 ... t_jk ) = μ + e[j₁] · D + e[j₂] · D + … + e[j_k] · D =

= μ + (e[j₁] · D + e[j₂] · D + … + e[j_k] ) · D = μ + f(σ) · D.

Вектор f(σ) = e[j₁] · D + e[j₂] · D + … + e[j_k] называется вектором запусков последовательности t_j1 t_j2 ... t_jk . Тогда i-й элемент вектора f(σ), f(σ)_i – это число запусков перехода t_i в последовательности t_j1 t_j2 ... t_jk . Вектор запусков, следовательно, является вектором с неотрицательными целыми компонентами. (Вектор f(σ) – это отображение Пaрихa последовательности .)

Покажем полезность матричного подхода к сетям Петри решением задачи сохранения: является ли данная маркированная сеть Петри сохраняющей? Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть w – n 1 – вектор-столбец. Тогда, если μ – начальная маркировка, а μ' – произвольная достижимая маркировка, необходимо, чтобы μ · w = μ' · w. Теперь, поскольку μ' достижима, существует последовательность запусков переходов σ, которая переводит сеть из μ в μ'. Поэтому

μ' = δ(μ, σ) = μ + f(σ) · D.

Следовательно, μ · w = μ' · w = (μ + f(σ) · D)· w = μ · w + f(σ) · D · w, поэтому f(σ) · D · w = 0.

Поскольку это должно быть верно для всех f(σ), имеем D · w = 0.

Таким образом, сеть Петри является сохраняющей тогда и только тогда, когда существует такой положительный вектор w, что D · w = 0. Это обеспечивает простой алгоритм проверки сохранения, а также позволяет получать вектор взвешивания w.

С помощью матричного подхода можно решить и проблему достижимости. Предположим, что маркировка μ' достижима из маркировки μ. Тогда существует последовательность (возможно, пустая) запусков переходов σ, которая приводит из μ к μ'. Это означает, что f(σ) является неотрицательным целым решением следующего матричного уравнения для х:

μ' = μ + x · D. (*)

Следовательно, если μ' достижима из μ, тогда уравнение (*) имеет решение в неотрицательных целых; если уравнение (*) не имеет решения, тогда μ' недостижима из μ.

ПРИМЕР: Рассмотрим маркированную сеть Петри на рис. 3.17.

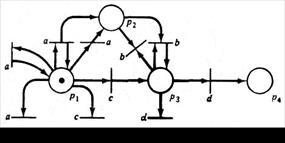
Рис. 3.16. Маркированная сеть Петри Рис. 3.17. Сеть Петри

Матрицы D ^–, D ⁺ и D имеют вид:

, , .

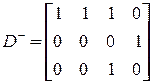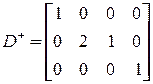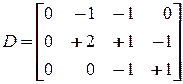В начальной маркировке μ = (1, 0, 1, 0) переход t₃ разрешен и приводит к маркировке μ', где

μ' = (1, 0, 1, 0) + (0, 0, 1) · 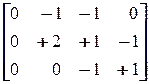= (1, 0, 1, 0) + (0, 0, –1, 1) = (1, 0, 0, 1).

Последовательность σ = t₃t₂t₃t₂t₁ представляется вектором запусков f(σ) = (1, 2, 2) и получает маркировку μ':

= (1, 0, 1, 0) + (1, 2, 2) · 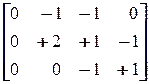= (1, 0, 1, 0) + (0, 3, –1, 0) = (1, 3, 0, 0).

Для определения того, является ли маркировка (1, 8, 0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение

(1, 8, 0, 1) = (1,0, 1, 0) + х · 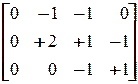, (0, 8, –1, 1) = х · ,

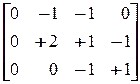которое имеет решение х = (0, 4, 5). Это соответствует последовательности
σ = t₃t₂t₃t₂t₃t₂t₃t₂t₁.

Можно показать, что маркировка (1, 7, 0, 1) недостижима из маркировки (1, 0, 1, 0), поскольку матричное уравнение

(1, 7, 0, 1) = (1,0, 1, 0) + х · 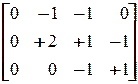, (0, 7, –1, 1) = х ·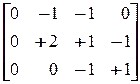

не имеет решения.

Упражнения

1. Построить матрицы D ^–, D ⁺ и D сети Петри с рис.3.6, рис.3.11, рис. 3.13.

2. Для сети Петри с рис.3.6 определить вектор запусков последовательности t₁t₁t₁t₂t₃t₃ и определить по формуле соответствующую маркировку μ'.

3. Для сети Петри С=(Р, Т, I, О), P = {p₁, p₂, p₃}, T = {t₁, t₂}, I(t₁) = {p₁, p₃}, I(t₂) = {p₂}, O(t₁) = {p₂}, O(t₂) = { p₁, p₃} с начальной маркировкой μ = (1, 0, 1) проверить свойство сохранения.

4. Для сети Петри из упражнения 3 с начальной маркировкой μ = (5, 0, 10) проверить по формуле достижимость маркировок μ' = (0, 5, 5), μ'' = (1, 1, 1).