Алгоритм получения обратной матрицы

1. Вычисление det A;

2. Транспонирование матрицы ;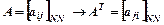

3. Определение алгебраических дополнений А_ji, j=1, N; i=1, N;

4. Составление союзной матрицы ;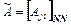

5. Вычисление обратной матрицы

;

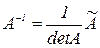
6. Проверка А^-1А=Е.

Существуют другие, более удобные способы вычисления обратной матрицы, например, методом Жордана – Гаусса, с которым познакомимся позднее.

Классический метод получения обратной матрицы

Пусть данная матрица:

.

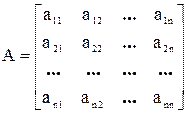Транспортируем ее .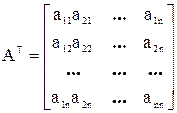

Найдем для каждого элемента а_ji транспортированной матрицы А^Т алгебраические дополнения А_ji.

Теперь составим для матрицы А так называемую присоединенную (или союзную) матрицу

.

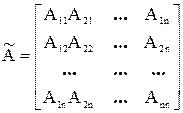Обратная матрица будет равна

.

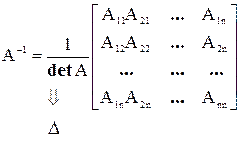Например: найти обратную матрицу для матрицы третьего порядка.

.

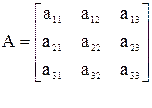
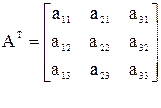
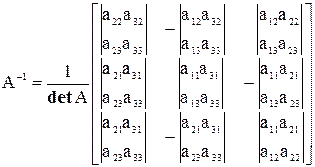Основные свойства обратной матрицы

1. Учитывая, что det(AB)=detA∙ detB, можем записать detA^-1 detA=detE=1.

Отсюда

.

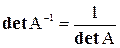Определитель обратной матрицы равен обратной величине определителя исходной матрицы.

2. (АВ)^-1=В^-1А^-1

3. (А^-1)=(A¹)^-1.

Тема 2.1. Теория графов в электроэнергетике