Транспонированная матрица

Если в матрице 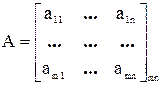строки и столбцы поменять местами, то получим транспонированную матрицу.

Свойства:

1) дважды транспонированная матрица равна исходной

А^{‌ ‌} = (А^‌ )^‌ = А;

2) (А+В)^‌ =А^‌ + В^‌ ;

3) (АВ)^‌ =В^‌ А^‌ , т.е. (АВ)^‌ ≠ А^‌ В^‌ ;

4) Если А^‌ =А, то матрица А^‌ - симметричная

(а_ij = a_ji)

Обратная матрица

Обратной матрицей по отношению к данной квадратной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Обозначим для матрица А обратную ей матрицу через А^-1.

АА^-1=А^-1А=Е.

Нахождение обратной матрицы для данной называется обращением данной матрицы.

Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы.

Пусть имеем матричное равенство

АС=В.

Умножим правую и левую часть равенства на обратную матрицу А^-1

А^-1АС= А^-1В.

Поскольку известно, что А^-1А=Е, то

ЕС= А^-1В.

И поскольку известно, что ЕС=С, то

С= А^-1В.

То есть, мы равенство АС=В преобразовали в равенство С= А^-1В, выразив матрицу С.

Если бы у нас были простые алгебраические числа а, b и с, то аналогичные преобразования были бы следующие: .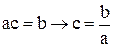

Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.