Миноры и алгебраические дополнения
Некоторые сведения из теории матричной алгебры
Классификация матриц
Система m n чисел, действительных или комплексных, расположенных в прямоугольной таблице из m строк и n столбцов называется матрицей
.
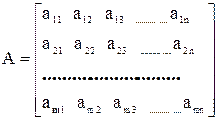где aij – элементы матрицы;
i = 1, 2, 3,…., m – номера строк;
m – число строк в матрице;
j = 1, 2, 3,…., n – номера столбцов;
n – число столбцов.
Для матрицы часто используется сокращенная запись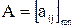 
, где m·n – размерность матрицы.
Если m = n (m ≠ 1, n ≠ 1), то матрица называется квадратной.
Если m ≠ n (m ≠ 1, n ≠ 1), то матрица называется прямоугольной.
Если m = n = 1, то матрица - скаляр.
Если m = 1, а n ≠ 1, то матрица называется вектор-строкой
.
Если n = 1, а m ≠ 1, то матрица называется вектор-столбцом
.
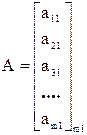Матрица нулевого порядка смысла не имеет.
Квадратная матрица, у которой диагональные элементы не равны нулю, а все недиагональные элементы равны нулю, называются диагональной
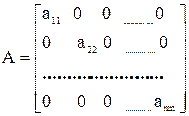
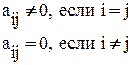
Диагональная матрица, у которой все ненулевые элементы равны единице, называется единичной и обозначается Е
.
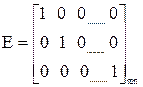Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О
.
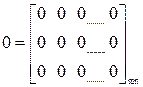Определитель
Определитель (или детерминант) является важной числовой характеристикой квадратной матрицы, обозначается через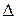 
или det A и вычисляется по известным правилам. Классический способ вычисления 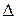(первый способ)
,
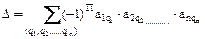где q1,q2,…,qn – произвольная перестановка вторых индексов;
П – число беспорядков в перестановке вторых индексов.
Число слагаемых произведений равно числу возможных перестановок вторых индексов, т.е. равно n!, где n - порядок квадратной матрицы.
Пример:
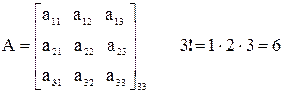
| Возможные перестановки вторых индексов | Число беспорядков | |
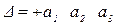
| 1) 1 2 3 | П=0 |
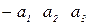
| 2) 1 3 2 | П=1 |
|
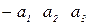
| 3) 2 1 3 | П=1 |
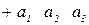
| 4) 2 3 1 | П=2 |
|
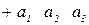
| 5) 3 1 2 | П=2 |
|
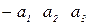
| 6) 3 2 1 | П=3 |
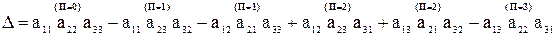
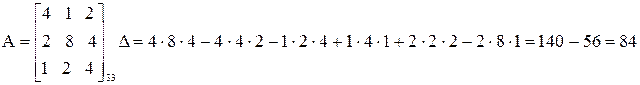
Число слагаемых произведений при вычислении Δ возрастает стремительно с увеличением n:
n = 2 2! = 2
n = 3 3! = 6
n = 4 4! = 24
n = 5 5! = 120
n = 6 6! = 720
Вычислять Δ классическим способом сложно и поэтому применяют другие способы.
Вычисление Δ для матрицы второго порядка (n = 2).
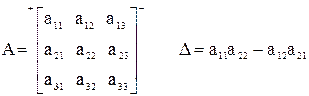
Два частных способа вычисления Δ для матриц только третьего порядка (n = 3).
|
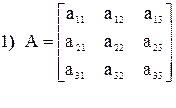
Слагаемые произведения со знаком +
|
|
|
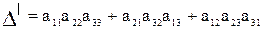
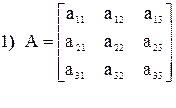
Слагаемые произведения со знаком -
|
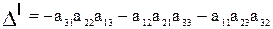
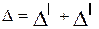
| 2) |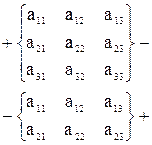 
|
Указанные схемы вычисления Δ для матриц второго и третьего порядков основаны на использовании геометрического расположения элементов в матрицах, что неприменимо для матриц более высокого порядка.
Миноры и алгебраические дополнения
Минором Мij элемента аij матрицы А, называется определитель матрицы (n-1)-ого порядка, полученной из матрицы А путем вычеркивания i-й строки и j-го столбца.
Алгебраическим дополнением называется минор, вычисляемый по формуле:
.
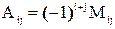Дата добавления: 2016-02-16; просмотров: 621;