Действия с матрицами

1. Сумма и разность матриц.

Могут складываться и вычитаться матрицы только одинакового типа.

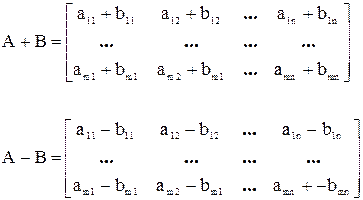
Из сложения матриц вытекают следующие свойства:

1) А+(В+С)=(А+В)+С;

2) А+В=В+А;

3) А+0=А.

2. Умножение матрицы на скаляр.

Отсюда: 1) 1А=А; 2) 0А=0;

3) α (β А) = (α_β) А; 4) αА + βА = (α+β) А;

5) α (А+В) = αА + αА;

3. Умножение матриц А * В = С.

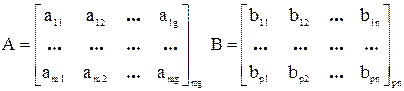
Перемножать матрицы можно только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы, т.е. g=p, а число строк первой матрицы и число столбцов второй матрицы могут быть любые, т.е. m≠n. Результатом будет матрица С размерностью mn, элементы которой

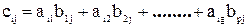
Для вычисления элемента, стоящего в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-ой строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и полученные произведения сложить.

Свойства:

1) А(ВС)=(АВ)С;

2) α(АВ)=(αА)В;

3) (А+В)=АС+АВ.

4)

Запомнить, что в общем случае 4) АВ≠ВА.

Пример:

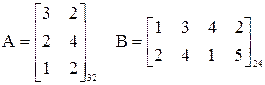
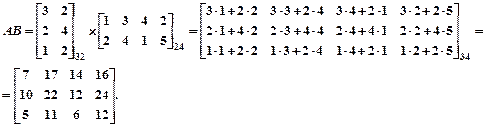
В тех частных случаях, когда АВ=ВА, матрицы А и В называются перестановочными. Например, единичная матрица Е перестановочна с любой матрицей А того же порядка.

АЕ=ЕА=А.

Единичная матрица Е играет роль единицы при умножении.