Затраты времени на чтение, матрица данных генеральной совокупности из пяти человек
| Единицы генеральной совокупности | Затраты времени на чтение в среднем за день, мин |
| 1. Иван | |
| 2. Петр | |
| З. Александр | |
| 4. Иосиф | |
| 5. Павел |
Искомая характеристика генеральной совокупности — средние затраты времени на чтение: 40 мин. Нормальные проектировщики выборки всего этого не знают — у них нет возможности обследовать всю генеральную совокупность из пяти семей — поэтому и начинают строить выборку. Допустим, что объем выборочной совокупности из 2 человек достаточен для заданного уровня надежности предсказания. Тогда мы можем начать процедуру отбора единиц исследования. Напомним, что все 5 человек имеют равные шансы быть опрошенны
26 Аналогичный пример рассматривается в учебнике Б.Ц. Урланиса «Общая теория статистики» (М.: Статистика, 1972), где элементы теории выборки изложены более подробно.
ми. Здесь не помешает и напоминание об аналогии социологического отбора со случайным процессом: как будто мы вынимаем из мешка шар и регистрируем его параметры. Поскольку объем выборки 2 человека, опросим Ивана и Павла, подсчитаем их средние затраты времени на чтение и зарегистрируем результат: 45 мин. Обследование завершено. В социологической практике опросы ограничиваются одной выборкой, а в нашем примере полезно осуществить и другие выборки из той же генеральной совокупности. Ведь кроме Ивана и Павла есть и иные единицы, имеющие такие же шансы быть обследованными. Произведем вторую выборку — опросим Ивана и Петра. Их средняя составит 15 мин. В третью выборку оба раза попал Павел — после регистрации результатов опроса единица возвращается в генеральную совокупность и может быть «вынута» вторично — такая выборка называется возвратной. Выборочная средняя «двойного» опроса Павла составляет 80 мин. Четвертый раз выпали Александр и Иосиф — средняя 45 мин. Предположим, в пятую выборку два раза вошел Иван, средняя составляет 10 мин. Мы видим, что все происходящее слишком случайно и, тем не менее, следует подсчитать ошибки выборки — разницу между значениями выборочной и генеральной совокупности по модулю (пока безразлично, какой знак имеет отклонение): 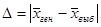 (табл. 5.9)
(табл. 5.9)
Таблица 5.9
Дата добавления: 2016-03-27; просмотров: 724;
