Абсолютный нуль температуры
Предельную температуру, при которой объем идеального газа становится равным нулю, принимают за абсолютный нуль температуры.
Найдем значение абсолютного нуля по шкале Цельсия.
Приравнивая объем V в формуле (3.1) нулю и учитывая, что
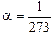 1/°С,
1/°С,
получим
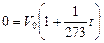 .
.
Отсюда абсолютный нуль температуры равен
t = –273 °С.2
Это предельная, самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказал Ломоносов.
_____________
[1]Наибольшие температуры на Земле – сотни миллионов градусов – получены при взрывах термоядерных бомб. Еще более высокие температуры характерны для внутренних областей некоторых звезд.
2Более точное значение абсолютного нуля: –273,15 °С.
Шкала Кельвина
Английский ученый У. Кельвин ввел абсолютную шкалу температур. Нулевая температура по шкале Кельвина соответствует абсолютному нулю, и единица температуры по этой шкале равна градусу по шкале Цельсия, поэтому абсолютная температура Т связана с температурой по шкале Цельсия формулой
 Т = t + 273. (3.2)
Т = t + 273. (3.2)
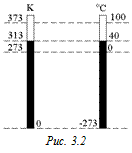
На рис. 3.2 для сравнения изображены абсолютная шкала и шкала Цельсия.
Единица абсолютной температуры в СИ называется кельвином (сокращенно К). Следовательно, один градус по шкале Цельсия равен одному градусу по шкале Кельвина:
1 °С = 1 К.
Таким образом, абсолютная температура по определению, даваемому формулой (3.2), является производной величиной, зависящей от температуры Цельсия и от экспериментально определяемого значения a.
Читатель: А какой физический смысл имеет абсолютная температура?
Автор: Согласно молекулярно-кинетической теории абсолютная температура прямо пропорциональна средней кинетической энергии хаотического движения атомов или молекул. При Т = 0 К тепловое движение молекул прекращается.
Запишем выражение (3.1) в виде
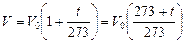 .
.
Учитывая, что температура по шкале Кельвина связана с температурой по шкале Цельсия соотношением Т = t + 273, получим
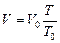 ,
,
где Т0 = 273 К, или
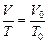 . (3.3)
. (3.3)
Поскольку это соотношение справедливо для произвольной температуры Т, то закон Гей-Люссака можно сформулировать так:
Для данной массы газа при р = const выполняется соотношение
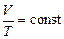 . (3.4)
. (3.4)
Задача 3.1. При температуре Т1 = 300 К объем газа V1 = 5,0 л. Определите объем газа при том же давлении и температуре Т = 400 К.
| V1 = 5,0 л Т1 = 300 К Т = 400 К | Решение.
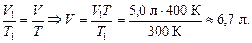 Ответ:
Ответ: 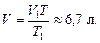
|
| V = ? | |
СТОП! Решите самостоятельно: А1, В6, С2.
Задача 3.2. При изобарическом нагревании объем воздуха увеличился на 1 %. На сколько процентов повысилась абсолютная температура?
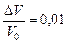
| Решение. Пусть начальная температура Т0, а объем V0. Тогда новая температура Т = Т0 + DТ, а объем V = V0 + DV. Согласно формуле (3.3)
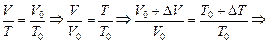
|
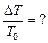
| |
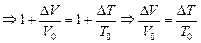 = 0,01.
= 0,01.
Ответ: 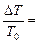 1 %.
1 %.
Запомним полученную формулу
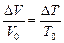 . (3.5)
. (3.5)
СТОП! Решите самостоятельно: А2, А3, В1, В5.
Закон Шарля
Французский ученый Шарль экспериментально установил, что если нагревать газ так, чтобы его объем оставался постоянным, то давление газа будет увеличиваться. Зависимость давления от температуры имеет вид:
р(t) = p0(1 + bt), (3.6)
где р(t) – давление при температуре t °С; р0 – давление при 0 °С; b – температурный коэффициент давления, который одинаков для всех газов: 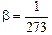 1/К.
1/К.
Читатель: Удивительно, что температурный коэффициент давления b в точности равен температурному коэффициенту объемного расширения a!
Автор: На самом деле, зная законы Бойля–Мариотта и Гей-Люссака, это можно доказать чисто теоретически, не прибегая ни к каким экспериментам!
Возьмем определенную массу газа объемом V0 при температуре Т0 и давлении р0. В первый раз, поддерживая давление газа постоянным, нагреем его до температуры Т1. Тогда газ будет иметь объем V1 = V0(1 + at) и давление р0.
Во второй раз, поддерживая объем газа постоянным, нагреем его до той же температуры Т1. Тогда газ будет иметь давление р1 = р0(1 + bt) и объем V0.
Так как в обоих случаях температура газа одинакова, то справедлив закон Бойля–Мариотта:
p0V1 = p1V0 Þ р0V0(1 + at) = р0(1 + bt)V0 Þ
Þ 1 + at = 1 + bt Þ a = b.
Так что ничего удивительного в том, что a = b, нет!
Перепишем закон Шарля в виде
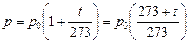 .
.
Учитывая, что Т = t °С + 273 °С, Т0 = 273 °С, получим
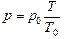 Þ
Þ 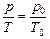 . (3.7)
. (3.7)
Закон Шарля можно сформулировать так:
Для данной массы газа при V = const справедливо соотношение
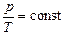 . (3.8)
. (3.8)
Процессы, происходящие при неизменном объеме, называются изохорическими. Закон Шарля описывает изохорический процесс.
Задача 3.3. При изготовлении электроламп их наполняют инертным газом при температуре t1 = 150 °С. Под каким давлением должны заполняться лампы, чтобы при температуре t2 = 300 °С, которая устанавливается в лампе при горении, давление было равно р2 = 0,10 МПа?
| t1 = 150 °С ÞТ1 = 423 К t2 = 300 °С Þ Т2 = 573 К р2 = 0,10 МПа = = 0,10×106 Па | Решение. 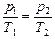 , отсюда , отсюда
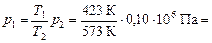 = 0,74×105 Па.
Ответ:
= 0,74×105 Па.
Ответ: 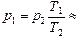 0,74×105 Па. 0,74×105 Па.
|
| р1 = ? | |
СТОП! Решите самостоятельно: А6, А8, В7, В9.
Дата добавления: 2016-04-11; просмотров: 3228;
