Влияние температуры
(с точки зрения принципа Ле Шателье)
1. а) Наконец, рассмотрим влияние на ход реакции повышения или понижения температуры. Заметим: в одном направлении почти любая реакция является экзотермической, а в противоположном направлении – эндотермической.
Следовательно, применительно к температуре принцип Ле Шателье выглядит следующим образом: нагревание должно ускорять эндотермическое направление реакции (для которого ΔНрц> 0), а охлаждение – экзотермическое направление (для которого ΔНрц< 0).
б) Действительно, ускорение эндотермического направления (при нагревании) приводит к связыванию части подводимой к системе теплоты, что ослабляет исходное повышение температуры.
2. Однако следует иметь в виду важную особенность.
а) Из-за ускорения одного из направлений реакции концентрации участников изменяются, поэтому в новом состоянии равновесия (при новой температуре) отношение концентраций уже не то, что прежде. Таким образом, нагревание ведёт к изменению константы равновесия, а значит, и к сдвигу положения равновесия (чего, как уже отмечалось, не было при концентрационных возмущениях и при изменении общего давления).
б) Более конкретно это выглядит так:

В самом деле, если прямое направление реакции – эндотермическое (ΔНрц > 0), то из-за сдвига реакции в этом направлении (под действием нагревания) в системе увеличивается доля продуктов – константа равновесия возрастает (dKр/dT > 0). Аналогично влияет на равновесие введение в систему иной энергии – не тепловой, а, например, световой, если система способна поглощать эту энергию.
Обсудим также количественную сторону влияния температуры на термодинамические параметры реакции – ΔSрц, ΔGрц и Кр .
5.8. Влияние температуры на ΔSрц и ΔGрц
 |
1. а) В п. 2.5 было показано, что зависимость энтальпии реакции от температуры в изобарных условиях определяется величиной ΔСР – разностью молярных теплоёмкостей участников:
б) Так, если теплоёмкость продуктов – выше, чем реагентов (ΔСР > 0), то при нагревании системы всё больше теплоты остаётся в продуктах, и реакция (если она эндотермическая) требует больше теплоты – ΔHрц возрастает.
в) Был рассмотрен также пример, который показывал, что фактическая зависимость ΔHрц от температуры – довольно слабая, отчего ею обычно пренебрегают.
2. Такие же свойства присущи и энтропии реакции, ΔSрц .
а) Действительно, для нагревания 1 моля произвольного участника реакции
можно записать:

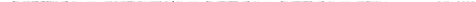 |
где S0— абсолютная энтропия вещества, а CP — его изобарная теплоемкость.
б) Тогда для энтропии реакции (на примере простейшей реакции A → B) получаем:
 |
что дает уравнение
сходное с (2.29).
в) Таким образом, и для энтропии реакции температурная зависимость опре-
деляется разностью теплоемкостей продуктов и реагентов. Из-за малости
данной разности зависимостью 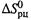 от температуры обычно тоже можно пренебречь.
от температуры обычно тоже можно пренебречь.
3. а) Обратимся к стандартной энергии Гиббса реакции:

(Заметим: в данном случае температура считается не стандартной — 298 К, — а произвольной.) Полагая, что 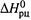 и
и 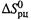 не зависят от температуры, получаем:
не зависят от температуры, получаем:
 |
б) Второе из этих выражений называется уравнением Гиббса-Гельмголъца(это дифференциальное уравнение относительно 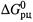 ).
).
в) Однако в данном случае более наглядно первое уравнение. Из него видно, что производная 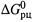 по температуре равна энтропии реакции, взятой с обратным знаком.
по температуре равна энтропии реакции, взятой с обратным знаком.
г) Это выражение весьма близко к формуле (4.20,а):
 |
устанавливающей, что температурная зависимость энергии Гиббса процесса
определяется энтропией системы. Но данная формула была выведена лишь для обратимых процессов.
 д) В отличие от этого, соотношение
д) В отличие от этого, соотношение
(5.13,а) справедливо для произвольных, в т.ч. и необратимых реакций. Правда, оно исходит из других упрощающих допущений —
независимости 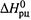 и
и 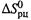 от температуры.
от температуры.
е) Итак, согласно (5.13,а), характер из-
менения 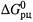 с ростом температуры
с ростом температуры
определяется знаком 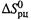 .
.
Если 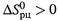 , то
, то 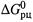 снижается (или становится более отрицательным), т.е. способность реакции к самопроизвольному протеканию увеличивается.
снижается (или становится более отрицательным), т.е. способность реакции к самопроизвольному протеканию увеличивается.
А если 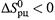 , то зависимость
, то зависимость 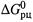 от температуры обратная (рис. 5.3).
от температуры обратная (рис. 5.3).
5.9. Зависимость Kp от температуры
1. Общий характер этой зависимости нам уже известен (5.8,а-б). Теперь
установим ее конкретный вид.
а) Выразим Kp из соотношения (4.35) и используем (5.12):

Видно, что, если 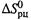 и
и 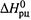 от температуры не зависят, то при росте температуры Kp стремится к некоторому предельному уровню (5.14,6), который при
от температуры не зависят, то при росте температуры Kp стремится к некоторому предельному уровню (5.14,6), который при 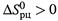 больше 1, а при
больше 1, а при 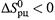 — меньше 1.
— меньше 1.
б) Для определения характера зависимости Kp от Т (убывание или возраста-
ние) продифференцируем формулу (5.14, а):


 |
откуда
Таким образом, знак производной 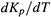
совпадает со знаком 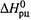 , что соответствует неравенствам (5.8,а-б) и показано на рис. 5.4. (Сравним: знак производной
, что соответствует неравенствам (5.8,а-б) и показано на рис. 5.4. (Сравним: знак производной 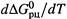 определяется знаком
определяется знаком 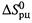 , но противоположенему (5.13,а).)
, но противоположенему (5.13,а).)
2. Уравнение, связывающее Kp с температурой, называют уравнением изобары химической реакции(или, наряду с уравнением изотермы химической реакции (4.34), — уравнением Вант-Гоффа). Его можно записать в разных формах.
 |
а) По сути дела, уже формула (5.14,а) являетсяуравнением изобары. Но
обычно ее представляют в логарифмическом виде:
 |
Чем полезно это выражение? Из него следует, что если
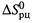 и
и 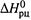 не зависят от температуры, то имеется линейная связьмежду
не зависят от температуры, то имеется линейная связьмежду 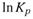 и
и 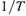 (рис. 5.5), причем на графике этой зависимости
(рис. 5.5), причем на графике этой зависимости
 б) Следовательно, если экспериментально найти константу равновесия реакции
б) Следовательно, если экспериментально найти константу равновесия реакции
при нескольких температурах и построить график в указанных координатах, то по тангенсу угла наклона прямой можно найти энтальпию реакции.
Вместе с тем можно найти также стандартную энергию Гиббса (при какой-то температуре 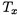 ) и энтропию реакции:
) и энтропию реакции:

в) Причем, достаточно ограничиться всего двумя точками, т. е. измерить Kp при двух температурах — T1 и T2.
 |
Действительно, запишем уравнение (5.16) для температуры T1, затем — для
температуры T2 и вычтем одно уравнение из другого. Тогда член
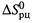 сокращается, и получается:
сокращается, и получается:
Это еще одна форма уравнения изобары химической реакции. С ее помощью,
зная Kp1 и Kp2 (при температурах T1 и T2), нетрудно рассчитать 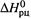 .…
.…
 |
3. Наиболее общей формой уравнения изобарысчитается уравнение (5.15,6), если в нем перенести Kp из правой части в левую и взять под знак дифференциала (то же получается при дифференцировании формулы (5.16)):
Здесь в самом сжатом виде определена температурная зависимость Kp.
Краткое содержание главы 5
Глава посвящена ХИМИЧЕСКОМУ РАВНОВЕСИЮ.
1. Так, в ней сформулированы законы, касающиеся химического равновесия.
а) ЗАКОН ДЕЙСТВУЮЩИХ МАСС – отношение концентраций при равновесии не зависит от их исходных значений:
 |
 |
б) ЗАКОН ГЕССА ДЛЯ КОНСТАНТ РАВНОВЕСИЯ – для альтернативных цепей реакций равны произведения констант равновесия:
в) ПРИНЦИП ЛЕ ШАТЕЛЬЕ — в ответ на некоторое возмущение (изменение концентраций, общего давления или температуры) в обратимой реакции усиливается одно из двух направлений — и результат внешнего воздействия частично ослабевает.
2. Кроме того, мы установили количественную ЗАВИСИМОСТЬ ОТ ТЕМПЕРАТУРЫ термодинамических параметров реакции.
а) В случае ЭНТРОПИИ зависимость является слабой (из-за малости 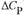 ), а в случае ЭНЕРГИИ ГИББСА — почти линейной:
), а в случае ЭНЕРГИИ ГИББСА — почти линейной:
 |
б) Для КОНСТАНТЫ же РАВНОВЕСИЯ получена серия соотношений, из которых наиболее важны следующие:
 Таким образом, зная Крпри двух температурах, можно найти ΔНорц.
Таким образом, зная Крпри двух температурах, можно найти ΔНорц.
ЗАДАЧИ К РАЗДЕЛУ 1
1. При t = 180° С 4 г водорода занимают объём V1 = 3л. Определить работу при изотермическом расширении этого количества водорода до объёма V2 = 4,8 л.
Решение
Имеется n = m/M(H2) = 2 моля водорода. Искомая работа, согласно (1.6) и с учётом того, что R ≈ 8,31 Дж/(моль∙К), а Т = 453 К, такова:
w = – nRT ln(V2 /V1) = 3,53 кДж. (I.1)
2. Рассчитать разность теплот QP – QV(на 1 моль ацетальдегида или на 1 моль этанола) при Т1 = 298 К и (отдельно) при Т2 = 400 К для реакции
Ацетальдегид (г)+H2 (г)= Этанол(при Т1 – ж; при Т2 – г).
Решение
а) Исходя из (1.10), (1.11) и (2.5), разность теплот изобарного (QP) и изохорного (QV) проведения реакции равна работе расширения (или сжатия) газа:
QP – QV = –wP = PΔV = ΔnгазRT , (I.2)
где Δnгаз – изменение количества газообразных веществ в системе.
б) В расчёте на 1 моль реагирующего ацетальдегида или на 1 моль образующегося этанола, количество газообразных веществ снижается при Т1 на 2 моля (Δnгаз = –2), а при Т2 – на1 моль (Δnгаз = –1).
в) В итоге, подстановка величин в (I.2) даёт: искомая разность теплот при Т1 равна –4,95 кДж/моль, а при Т2 – –3,32 кДж/моль.
3. Для метана ΔНообр = –74,85 кДж/моль. Определить ΔЕообр метана.
Решение
а) Реакция образования метана: 2Н2 + С = СН4 .
В расчёте на 1 моль образующегося метана, Δnгаз = –1.
б) Исходя из (2.8) и учитывая, что Т =298 К, получаем:
ΔEообр= ΔНообр – PΔV = ΔНообр – ΔnгазRT = –72,37 кДж/моль . (I.3)
4. Найти ΔE при испарении m = 0,2 кг этанола при температуре кипения (tк = 78,3°С). Теплота парообразования при той же температуре – Q1 кг = 856,9 кДж/кг. Изменением объёма жидкой фазы спирта пренебречь.
Решение
а) Согласно (1.7),
ΔE = m(Q1 кг + w) = m(Q1 – PΔV1 кг), (I.4)
где ΔV1 кг – увеличение парциального объёма, занимаемого испаряющимися молекулами (в расчёте на 1 кг вещества).
б) Перейдём к ΔV1 моль (изменению объёма в расчёте на 1 моль вещества):
ΔV1 кг = ΔV1 моль / M ; (I.5)
здесь М – молярная масса этанола.
в) Тогда, в соответствии с (2.5),
PΔV1 моль = ΔnгазRT, где Δnгаз =1,
откуда
ΔE = m(Q1 – RT / M) ≈ 159 кДж. (I.6)
Здесь учтено, что Тк = 351,3 К и М = 46 г/моль = 0,046 кг/моль.
5. Расcчитать ΔН нижеследующей реакции при Т = 500 К, используя значения ΔНообр и СР её реагентов и продуктов:
2NaBr (кр) + Сl2 (г) = 2NaCl (кр) +Br2 (ж)
ΔНообр , кДж/моль - 365 0 -411 0
СР , Дж/(моль∙К) 88,3 33,9 50,9 75,7
Решение
а) В соответствии с формулой (2.18,а), при стандартной температуре (25оС, или 298 К) энтальпия реакции равна
ΔНорц = 2 ΔНообр (NaCl) – 2 ΔНообр (NaBr) = – 92 кДж/моль. (I.7)
б) Находим также разность теплоёмкостей продуктов и реагентов (2.27):
ΔСР = 2 СР (NaCl) + СР (Br2) – 2 СР (NaBr) – СР (Cl2) = –33 Дж/(моль∙К) . (I.8)
в) Энтальпию реакции при указанной в задаче температуре (для которой ΔТ = 202 К) оцениваем по формуле Кирхгофа(2.27):
ΔНрц (500 K) ≈ ΔНорц + ΔСР∙ΔТ ≈ – 99 кДж/моль (I.9)
6. Найти ΔS для превращения m = 1 г жидкой воды при Т1 = 273 К в пар при Т2 = 423 К. Давление считать нормальным: Р = 1 атм = 101,3 кПа (1.3). Теплоёмкость жидкой воды – СР(ж) ≈ 4,18 Дж/(г∙К) (2.26), а водяного пара – СР(г) ≈ 1,99 Дж/(г∙К). Теплота испарения при температуре кипения – ΔНисп = 40 кДж/ моль (3.18).
Решение
а) Последнюю величину отнесём к 1г воды:
ΔНисп = 40 кДж/моль : 18 г/моль = 2,25 кДж/г (I.10)
б) По аналогии с формулой (3.19), результирующее изменение энтропии рассчитывается как сумма ΔSi трёх процессов:
- нагревания жидкой воды от 0 до 100оС (т.е. от 273 К до 373 К),
- испарения воды при 100оС (373 К)
- и нагревания водяного пара от 100оС до 150оС (от 373 К до 423 К):
Ткип Т2
ΔS = СР(ж)∫dT / T+ΔНисп/Tкип + СР(г) ∫dT / T = (I.11,a)
Т1 Ткип
= СР(ж) ln(Tкип /T1 ) +ΔНисп/Tкип + СР(г) ln(T2 /Tкип ) ≈ 7,59 Дж/(г∙К) . (I.11,б)
7. Рассчитать ΔS после смешивания двух порций спирта (m1 = 2,3 г, t1 = 70оC; m2 = 5,8 г, t2 = 10оC) и выравнивания их температур (до tср). Молярная теплоёмкость спирта – С = 111,4 Дж/(моль∙К). Изменением объёма системы пренебречь.
Решение
а) Количество теплоты, отданной первой (более горячей) порцией, равно по абсолютной величине количеству теплоты, полученной второй порцией спирта:
–Q1 = Q2 , или, согласно (2.20,а), m1С (t1 – tср) = m2С (tср – t2) . (I.12)
Отсюда
tср = (m1 t1 + m2 t2 ) /(m1 + m2) = 27oC; Тср = 300 K . (I.13)
б) Изменение энтропии каждой порции, согласно (3.14), таково:
ΔS1 = n1 ∙С∙ln(Tср /T1) = (m1/M)∙C∙ln(Tср /T1) = –0,73 Дж/К , (I.14,a)
ΔS2 = n2 ∙С∙ ln(Tср /T2) = (m2/M)∙C∙ ln(Tср /T2) = +0,97 Дж/К , (I.14,б)
где М = 46 г/моль – молярная масса этанола, Т1 = 343 К, Т2 = 283 К. Энтропия остывающей порции уменьшается, а нагревающейся порции – возрастает.
в) Результирующее изменение энтропии системы – положительная величина:
ΔS = ΔS1 + ΔS2 = +0,24 Дж/K . (I.15)
Это иллюстрирует второе начало термодинамики в отношении процессов теплопередачи. – Итогом таких процессов является не только переход теплоты от более тёплого объекта к более холодному (что выравнивает температуры), но и возрастание энтропии системы в целом.
8. Вычислить ΔGо для следующей реакции (при 25оС), используя нижеприведённые термодинамические данные:
СО2 (г)+ 4 Н2(г)= СН4(г)+ 2 Н2О(ж)
ΔНообр , кДж/моль –394 0 –75 –286
Sо, Дж/(моль∙К) 214 131 186 70
Решение
а) Найдём вначале энтальпию (теплоту) реакции (по формуле 2.18,а):
ΔНорц = ΔНообр(СН4) + 2 ΔНообр(Н2О) – ΔНообр(СО2) = – 253 кДж/моль. (I.16)
б) Оценим также изменение энтропии в ходе реакции. В условии задачи приведены значения абсолютной энтропии соответствующих веществ. Очевидно, для них справедлива формула, аналогичная (2.18,а):
ΔSорц = Sо(СН4) + 2 Sо(Н2О) – Sо(СО2) – 4 Sо(H2) = – 412 Дж/(моль∙К). (I.17)
в) Тогда, полагая Т = 298 К, для стандартной энергии Гиббса реакции получаем (5.12):
ΔGорц = ΔНорц – TΔSорц = –130 кДж/моль .(I.18)
Значительное отрицательное значение энергии Гиббса свидетельствует о том, что при соответствующих кинетических условиях реакция может самопроизвольно протекать в прямом направлении.
г) Но заметим, что этот итог достигается за счёт лишь одного фактора – энтальпийного (выделения теплоты), тогда как второй фактор (энтропийный) оказывает противоположное (но более слабое) воздействие на общий баланс энергии Гиббса. Т.е. протекание реакции в прямом направлении сопровождается не ростом, а снижением энтропии. Действительно, в ходе реакции 5 молекул двух газов преобразуются лишь в 2 молекулы третьего газа и молекулу жидкости. Т.е. степень свободы (разупорядоченность) системы существенно понижается.
9. В закрытом сосуде идёт обратимая реакция: N2O4 ↔ 2 NO2 .
При t = 25 оC её константа равновесия равна Кр = 0,1 моль/л. В каком направлении идёт реакция при следующих активностях веществ:
а(NO2) = 0,01 моль/л, а(N2O4) = 0,02 моль/л ?
Решение
а) «Произведение активностей» равно
Па = а(NO2)2 / а(N2O4) = 0,5 моль/л (I.19)
б) По уравнению изотермы (уравнению Вант-Гоффа) (4.34) определяем энергию Гиббса реакции:
ΔGрц = RT ln (Па/Kp) ≈ –7,4 кДж/моль. (I.20)
в) Т.к. ΔGрц < 0, равновесие реакции сдвинуто вправо.
10. Дана реакция:
NaOH (тв) + СО2(г) = Na2CO3 (тв) + Н2О(г) .
ΔGообр , кДж/моль –425 –394 –1060 –229
Может ли она протекать в прямом направлении при следующих условиях:
Т = 298 К, Р(СО2)= 10–5 атм, Р(Н2О)= 10–3 атм ?
Решение
а) Стандартная энергия Гиббса реакции (4.40,а):
ΔGорц = ΔGообр(Na2CO3) + ΔGообр(Н2О) – ΔGообр(NaOH) – ΔGообр(СО2) = –470 кДж/моль.
. (I.21)
б) Концентрационный член энергии Гиббса реакции (4.33):
RT ln Пс = RT ln [Р(Н2О) / P(СО2)] = RT ln102 = 11,4 кДж /моль. (1.22)
в) Итоговое значение энергии Гиббса реакции при указанных условиях – рассчитывается по уравнению изотермы (4.37):
ΔGрц = ΔGорц + RT ln Пс = –458,6 кДж/моль . (1.23)
Таким образом, прямая реакция является резко экзергонической и будет оставаться таковой при любых физически возможных парциальных давлениях СО2 и Н2О.
11. Пусть вновь (как в задаче 9) в закрытом сосуде идёт обратимая реакция:
N2O4 ↔ 2 NO2 .
При t = 55oC Кр = 1,38∙105 н/м2 (Па). (Заметим: для реакций в газовой среде Кр может выражаться не только в концентрационных единицах, как это было в задаче 9, но и в единицах давления.)
Сколько молей N2O4 надо поместить в сосуд объёмом V = 10л, чтобы после достижения равновесия концентрация продукта реакцииустановилась на уровне [NO2] = 0,1 моль/л ?
Решение
а) Уравнение Клайперона-Менделеева можно записать через концентрацию газа (3.23):
Р = nRT / V = cRT .
 |
б) С учётом этого, обозначая равновесные давления через Рр(Х), а равновесные концентрации – через [X], имеем:
где со(N2O4) – начальная концентрация N2O4, а Т = 328 К.
в) Отсюда
со(N2O4) = 0,5[NO2] + [NO2] 2RT / Кр ≈250 моль/м3 = 0,25 моль/л . (1.25)
Заметим: поскольку Кр выражена в н/м2, то концентрации веществ при расчёте должны быть выражены в моль/м3: [NO2] = 0,1 моль/л = 100 моль/м3 .
г) В итоге, искомое начальное количество N2O4 составляет
nо(N2O4) = со(N2O4)∙V ≈ 2,5 моля . (I.26)
12. Дана реакция:
CuSO4∙3H2O (тв) + 2 Н2О(г) ↔ CuSO4∙5H2O (тв) .
Для неё ∆Норц = –106,7 кДж/моль, и при Т1 = 303 К равновесное давление пара воды равно Р1(Н2О) = 1,45 кПа. Найти Кр при Т2 = 293 К.
Решение
а) Константа равновесия при исходной температуре:
Kр,1 = 1 / [Р1(Н2О)]2 ≈ 0,4756 кПа–2 . (I.27)
 |
б) Значение этой константы при другой температуре можно найти с помощью уравнения изобары химической реакции (5.19):
Как видно, при снижении температуры на 10 градусов константа равновесия рассматриваемой реакции возрастает более чем в 4 раза.
13. В закрытом сосуде идёт обратимая реакция: Н2О + СО ↔ СО2 + Н2 .
Для неё ∆Норц = 41,84 кДж/моль, и при Т1 = 1278 К константа равновесия равна Кр,1 = 1,62. Изначально в сосуд внесено по 1 молю Н2О и СО. Найти количество Н2О и СО в сосуде после достижения равновесия при Т2 = 80.
Решение
 |
а) Как и в предыдущей задаче, по уравнению изобары химической реакции находим константу равновесия при второй температуре:
 |
б) С другой стороны, эта константа, по определению, равна
Здесь nр(Х) = [X]∙V – количество (в молях) компонента Х в сосуде после достижения системой равновесного состояния.
Т.к. реагенты введены в систему в одинаковых количествах (no(СО) = nо(H2O) = 1 моль), то, исходя из стехиометрии реакции, величины nр(Х) попарно равны (для реагентов и для продуктов):
nр(СО) = nр(H2O), nр(СО2) = nр(H2) .
Причём, появляющееся в системе количество каждого из продуктов равно убыли количества каждого из реагентов; в частности
nр(СО2) = no(СО) – nр(СО).
Всё это учтено в преобразованиях (I.30).
в) Выражая из конечного соотношения np(СО), получаем искомое содержание СО в сосуде при равновесном состоянии системы:
 |
nр(СО) = no(СО) / (√Kp + 1) ≈ 0,718 моля . (I.31)
Таково же и равновесное содержание воды.
РАЗДЕЛ 2.
Дата добавления: 2016-03-20; просмотров: 2336;
