Частные случаи условия химического равновесия
Между фазами
Ситуация 1. Фазы образованы двумя несмешивающимися жидкостями,
в каждой из которых растворено вещество Yi, причем последнее взаимодей-
ствует с обоими растворителями одинаково.
а) В этом случае перенос растворенного вещества из одной фазы в другую
означает совершение только осмотической работы.
Формула (4.27) позволяет записать:

б) Равенство не изменится, если к правой его части добавить и одновременно вычесть из неё некую величину 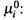

Сопоставление результата с (6.3) дает возможность получить выражения для
химического потенциала вещества Yiв той или иной фазе:

и позволяет сделать два важных вывода.
в) I. Во-первых, химический потенциал вещества зависит от концентрации последнего. (Данный вывод, как видим, — естественное следствие формулы (4.27) для осмотической работы.) При этом величина 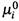 — стандартный химический потенциал, т.е. потенциал вещества Yiпри единичной (одномолярной) концентрации.
— стандартный химический потенциал, т.е. потенциал вещества Yiпри единичной (одномолярной) концентрации.
II. Второй же вывод следует из подстановки выражений (6.7) в равенство
(6.4, б). Такая подстановка дает:
 |
(Поскольку речь идет о равновесии, для обозначения концентраций использованы квадратные скобки.) Таким образом, в данной ситуации условием
химического равновесия является просто равенство концентраций вещества Yiв
обеих фазах.
Замечание.
а) Часто выражения для химического потенциала вещества Yi записывают иначе ~ не через молярные концентрации, а через его молярные доли Xi или активности αi (эффективные значения молярной концентрации или молярной доли):

б) Переход к первой из этих формул основан на следующих определениях и выкладках:

откуда
в) Если отношение 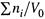 практически постоянно (при изменениях Xi), то содержащий его член ( RT ln[Σni/V0] ) можно (и необходимо!) включить в величину стандартного потенциала. Таким образом, стандартный потенциал в формулах (6.7) и (6.9) различен. В частности, в (6.9, а) — это химический потенциал вещества Yi при Xi = 1.
практически постоянно (при изменениях Xi), то содержащий его член ( RT ln[Σni/V0] ) можно (и необходимо!) включить в величину стандартного потенциала. Таким образом, стандартный потенциал в формулах (6.7) и (6.9) различен. В частности, в (6.9, а) — это химический потенциал вещества Yi при Xi = 1.
Ситуация 2. В системе, аналогичной предыдущей, растворенное вещество
Yiпо-разному взаимодействует с растворителями, образующими каждую из
фаз.
а) Указанное условие означает, что различны стандартные химические по-
тенциалы вещества в фазах (т. е. молярные энергии Гиббса вещества при его
одномолярных концентрациях):

 |
б) Если учесть это обстоятельство в выражениях (6.7), то условие химического равновесия (6.4, б) принимает вид:
Отсюда следует, что в состоянии химического равновесия концентрации
вещества Yi в фазах уже не одинаковы, концентрация выше там, где стандарт-
ный химический потенциал меньше.
в) Так, если в нашем примере 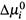 >0, т. е. стандартный потенциал меньше в фазе β, то, согласно (6.11, б), в этой фазе равновесная концентрация будет выше.
>0, т. е. стандартный потенциал меньше в фазе β, то, согласно (6.11, б), в этой фазе равновесная концентрация будет выше.
 |
г) Нетрудно найти и конкретную связь между равновесными концентрациями:
где Kр — одна из разновидностей констант равновесия, а именно — константа
распределения вещества Yiмежду фазами.
Ситуация 3. Одна фаза — раствор летучего вещества, вторая фаза — газо-
вая, куда вещество может испаряться с поверхности раствора.
а) Вообще говоря, принципиального отличия от предыдущего случая нет. Только химический потенциал вещества Yiв газовой фазе (пусть это фаза β) можно записать и через его парциальное давление, и через концентрацию:
 |
б) Однако стандартные потенциалы в этих двух записях различны: один (с чертой сверху) соответствует молярной энергии Гиббса вещества при его единичном
давлении, а другой — при единичной молярной концентрации в газовой фазе.
Ситуация 4. Рассматриваемое вещество находится не в газовом и не в рас-
творенном состоянии, а в жидком или твердом.
а) Здесь уже невозможно написать какое-либо выражение для химического потенциала (типа зависимости от концентрации или давления данного вещества).
Пример — система вода-лед. В этом случае можно только констатировать,
что при фазовом равновесии одинаковы химические потенциалы, т. е. моляр-
ные энергии Гиббса, жидкой воды и льда:

б) Это показывает, что данное условие фазового равновесия, т. е. условие вида (6.4,б), является более общим, чем, например, условие равенства концентраций. Поэтому именно оно используется при выводе правила фаз Гиббса.
Правило фаз Гиббса
1. Рассмотрим некую систему, включающую Ф фаз и К компонентов. Запишем сформулированные выше условия фазового равновесия:
 |
Как видим, в каждой строчке — по Ф переменных. Например, Tβ — температура фазы β, Tф— температура последней фазы (пронумерованной индексом Ф), 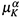 — химический потенциал К-то компонента в фазе α и т. д.
— химический потенциал К-то компонента в фазе α и т. д.
Всего же во всех строчках — (n + K)Ф переменных. Такое количество параметров характеризует рассмотренную систему.
2. Однако не все они независимы!
а) Так, в каждой строчке — по Ф — 1 уравнений связи, во всех строчках —
(n + K)(Ф - 1) уравнений связи.
б) Кроме того, для каждой фазы можно составить уравнения связи вида:
 |
где 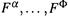 — известные числа или функции. Таким образом, присоединяется еще Ф уравнений.
— известные числа или функции. Таким образом, присоединяется еще Ф уравнений.
 |
в) Поясним смысл последних. Допустим, что
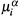 определяется просто кон-
определяется просто кон-центрацией вещества Yiв фазе α. Тогда в качестве
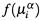 можно взять моляр-
можно взять моляр-ные доли Xi и записать для фазы α уравнение связи:
г) Другой пример: одна из фаз — смесь газов. В качестве 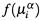 берем парциальное давление каждого газа и записываем для фазы α:
берем парциальное давление каждого газа и записываем для фазы α:
 |
где Pα — общее давление в фазе, уже фигурирующее в качестве переменной.
3. Итак, сколько же остается независимых переменных в нашей системе?
а) Обозначая данное число буквой С, находим:
 |
 |
откуда
Это и есть так называемое правило фаз Гиббса.
б) Величину С (количество независимых переменных) часто называют еще числом степеней свободы системы. Последнее показывает, сколько параметров (давление, температуру, концентрации) можно одновременно и произвольно(т.е. независимо друг от друга) менять, не изменяя числа или вида фаз равновесной системы .
в) Таким образом, главное здесь — сохранение прежнего фазового состояния при варьировании совокупности параметров. Если состояние остается устойчивым при одновременном варьировании большего числа параметров, степень свободы системы выше, и наоборот.
4. а) Согласно полученному правилу фаз, величина С тем больше, чем больше
внешних параметров (n), влияющих на систему, и чем больше компонентов (K)
в системе; но с увеличением числа фаз (Ф) в системе степень ее свободы уменьшается.
б) Всё это почти очевидно. Например, чем больше в системе компонентов, тем больше концентраций можно менять без нарушения фазового «портрета» системы, а значит, степень свободы выше. А чем больше фаз, тем более осторожными должны быть воздействия на систему для сохранения всех фаз, – степень свободы меньше.
5. а) Заметим также: если внешними факторами, влияющими на систему, являются (как это часто бывает) только давление и температура, то n = 2, и выражение (6.18,б) записывается в виде:

б) Если одна из этих величин тоже зафиксирована, то n = 1 и

Сформулированные в этой главе общие закономерности (условия фазового равновесия и правило фаз Гиббса) будут использованы в нескольких последующих главах для рассмотрения различных по сложности систем.
Краткое содержание главы 6
Главой 6 мы начали новый раздел – «ФАЗОВЫЕ РАВНОВЕСИЯ И РАСТВОРЫ НЕЭЛЕКТРОЛИТОВ».
1. Определены понятия ФАЗЫ и числа НЕЗАВИСИМЫХ компонентов. От общего количества компонентов последняя величина отличается на число математических связей:
К = К0 – х .
2. Сформулированы УСЛОВИЯ ФАЗОВОГО РАВНОВЕСИЯ. – Во избежание результирующего перемещения какого-либо компонента из одной фазы в другую, должны равняться не только температура и давление обеих фаз, но и ХИМИЧЕСКИЕ ПОТЕНЦИАЛЫ вещества в этих фазах:
μi ( α ) = μ i ( β ) .
 |
3. Для растворённого вещества химический потенциал зависит от его концентрации:
Поэтому условие равенства химических потенциалов может сводиться к равенству либо к определённому отношению концентраций вещества в фазах:
 |
4. Одно из ключевых обобщений – ПРАВИЛО ФАЗ ГИББСА (для системы, содержащей Ф фаз, К компонентов и зависящей от n внешних параметров):
C = K + n – Ф .
Оно определяет число степеней свободы системы, т.е. количество параметров, которые можно менять одновременно и произвольно, не изменяя числа и вида фаз равновесной системы.
Дата добавления: 2016-03-20; просмотров: 1081;
