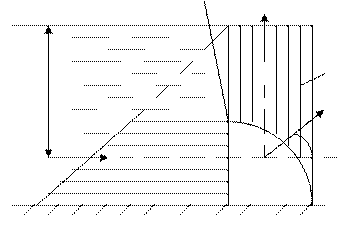
Сила давления жидкости на криволинейные поверхности
Определение давления жидкости на цилиндрическую поверхность представляет собой частный случай общей задачи о давлении жидкости на криволинейные поверхности. Чтобы получить общее решение, возьмём сосуд произвольной формы и выделим его на стенке какую-либо произвольную поверхность S, ограниченную контуром AMBN. Будем искать составляющие полного давления на эту поверхность по координатным осям, выбрав, например, начало координат на свободной поверхности жидкости и расположив оси так, как это показано на чертеже. При этом ограничимся определением лишь одной составляющей Rx. Параллельной оси x, поскольку остальные составляющие можно найти аналогичным образом. Найдём проекцию поверхности S на некоторую плоскость NN, нормальную к оси x и расположенную между этой поверхностью и координатной плоскостью ZOY. Отметим, что указанную плоскость проекции NN, как и направление самой оси x, можно выбирать по-разному. На жидкость, заключённую в объёме между поверхностью S, плоскостью NN и поверхностью проектирующего цилиндра, образующие которого параллельны оси x, действуют следующие силы: тяжести (вес) Gx выделенного объёма жидкости; давления жидкости RFx на проекцию поверхности S на плоскость NN; давления на боковую поверхность указанного объема (их проекция на ось x равна нулю); реакции R со стороны поверхности S, равная по значению, но обратная по направлению искомой силе давления жидкости. Проектируя эти силы на ось x, имеем:
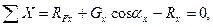 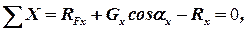
| (2.64) |
откуда для проекции силы реакции получаем
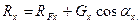 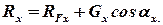
| (2.65) |
Аналогично находят выражения для проекции силы реакции и на другие координатные оси:
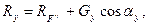 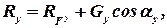
| (2.66) |
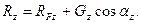 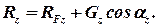
| (2.67) |
где ax , ay , az - углы между направлением линии действия силы тяжести и осями координат x, y, z.
Таким образом, получаем следующую общую теорему о давлении жидкости на криволинейную поверхность: проекция силы давления жидкости на криволинейную поверхность S на заданную ось x равна сумме проекций на эту ось веса жидкости, находящейся между поверхностью S, поверхностью проектирующего цилиндра и плоскостью проекций, нормальной к оси x, и силы давления жидкости на проекцию поверхности S на ту же плоскость проекции. Силу гидростатического давления на криволинейную поверхность определяют по формуле:
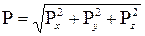 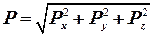 , ,
| (2.68) |
где 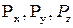 - составляющие силы избыточного давления по соответствующим координатным осям. В случае цилиндрической криволинейной поверхности:
- составляющие силы избыточного давления по соответствующим координатным осям. В случае цилиндрической криволинейной поверхности:
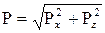 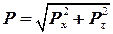 , ,
| (2.69) |
где PxPx и PzPy - горизонтальная и вертикальная составляющие силы P. Горизонтальная составляющая избыточного давления Px 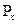 равна силе давления на вертикальную проекцию криволинейной поверхности:
равна силе давления на вертикальную проекцию криволинейной поверхности:
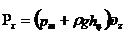 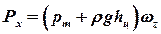 , ,
| (2.70) |
где pm- манометрическое давление на поверхности жидкости; hc - глубина погружения центра тяжести вертикальной проекции криволинейной поверхности; wz - площадь вертикальной проекции криволинейной поверхности. Если манометрическое давление на свободной поверхности жидкости равно нулю(p0 = pат), (P0 = Pат), то
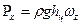 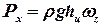 . .
| (2.71) |
Вертикальная составляющая Pz равна весу жидкости в объёме тела давления. Тело давления расположено между вертикальными плоскостями, проходящими через крайние образующие цилиндрической поверхности, самой цилиндрической поверхностью и свободной поверхностью жидкости или её продолжением. (рисуно 2.8)
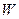
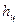
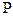
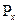
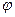
Рисунок 2.9 - -
Определение сил давления на криволинейную поверхность |
Если давление на свободной поверхности жидкости (P0 ≠ Pат),p0 ¹ pат, то тело давления ограничивается сверху пьезометрической плоскостью, удалённой от свободной поверхности жидкости на расстояние 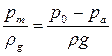
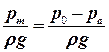 Направление силы PP определяется тангенсом угла j:j:
Направление силы PP определяется тангенсом угла j:j:
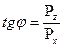 . .
| (2.72) |
Если криволинейная поверхность не цилиндрическая, то горизонтальную составляющую PyPy определяют аналогично PzPx..
Примеры и задачи
Пример 2.1.
Плотность и объем первой жидкости равны 1000 кг/м3 и 6 см3. Плотность и объем второй жидкости 800 кг/м3 и 4 см3. Определить плотность смеси этих жидкостей.
Решение:
По определению плотности масса первой и второй жидкости равны:
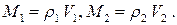
Плотность смеси находим по определению:
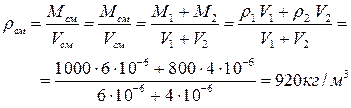
Ответ: плотность смеси равна 920 кг/м3
Пример 2.2.
Проводятся гидравлические испытания водопровода длиной 5 км и диаметром 2 м. Необходимо повысить давление в нём до 4 МПа. Какой объём воды необходимо дополнительно закачать в водопровод? Коэффициенты объёмного сжатия принять равными 5 10-10 1/Па.
Решение:
Из определения коэффициента объёмного сжатия жидкости следует, что изменение объёма воды равно 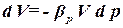 . Объём жидкости в трубе – это объём цилиндра диаметром D и длиной ℓ. Поэтому
. Объём жидкости в трубе – это объём цилиндра диаметром D и длиной ℓ. Поэтому
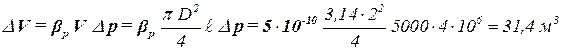
Ответ: необходимо закачать 31,4 м3 воды.
Пример 2.3.
Определить плотность воды при температуре 44 Сº, если при температуре 4 Сº плотность воды 1000 кг/м3. Коэффициент температурного расширения воды принять равными 4,8 10-4 1/Сº.
Решение:
Обозначим величины при температуре 4 Сº индексом 1, а при температуре плотность 44 Сº индексом 2. Тогда плотность жидкости при температуре 44 Сº равна:
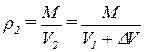 .
.
Изменение объёма воды при изменении температуры найдём из определения коэффициента температурного расширения: 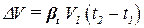 .
.
Тогда плотность воды будет равна:
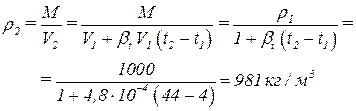 .
.
Ответ: плотность воды при температуре 44 Сº равна 981 кг/м3.
Пример 2.4.
В баке компрессора воздух находится при давлении 0,2 МПа и температуре 20 Сº. В баке образовалось отверстие, через которое происходит истечение воздуха в атмосферу (pат = 0,1 МПа). Определить температуру вытекающего воздуха.
Указание: процесс истечения считать адиабатическим (k = 1,5).
Решение:
Обозначим величины в баке компрессора индексом 1, а истекающего воздуха индексом 2. Запишем уравнения состояния и уравнение процесса:
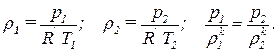
Из этих уравнений исключаем плотности:
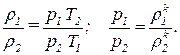
Откуда:
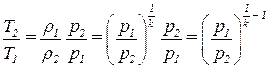 .
.
Тогда температура воздуха при истечении равна
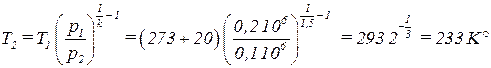 .
.
Или 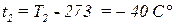
Ответ: температура истекающего воздуха равна - 40 .
Пример 2.5.
Вертикальная стенка длиной ℓ=3 м (в направлении, перпендикулярном плоскости чертежа), шириной b = 0,7 м и высотой Н0 = 2,5 м разделяет бассейн с водой на две части. В левой части поддерживается уровень воды H1 =2 м, в правой - H2 = 0,8 м.
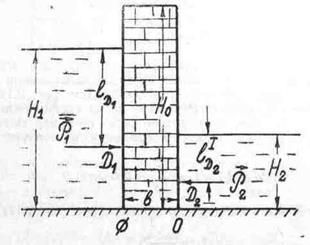 Рисунок 2.10 - - Схема к примеру 2.5 Рисунок 2.10 - - Схема к примеру 2.5
|
Найти величину опрокидывающего момента, действующего на стенку, а также определить, будет ли стенка устойчива против опрокидывания, если плотность материала стенки ρ = 2500 кг/м3.
Решение:
Найдем силу давления воды на стенку слева. Так как на поверхности давление атмосферное, то пьезометрическая плоскость совпадает с поверхностью жидкости,
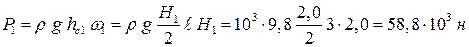 .
.
Стенка вертикальная, поэтому расстояние от линии уреза до центра тяжести равно глубине погружения центра тяжести ℓc1 = hc1 = H1/2. Момент инерции поверхности относительно линии, параллельной линии уреза и проходящей через центр тяжести равен 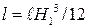 .
.
Тогда координата центра давления:
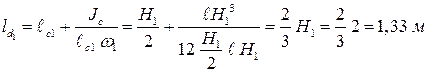 .
.
Точно также справа
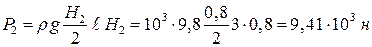 kH,
kH,
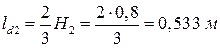 M.
M.
Опрокидывающий момент, то есть момент сил давления жидкости относительно точки О (см. рисунок 2.9), равен:
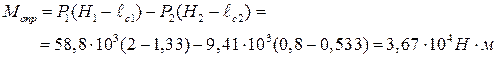
Устойчивость против опрокидывания сообщает стенке момент ее силы тяжести относительно точки О, равный:
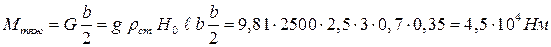
Так как Mтяж > Mопр, то стенка устойчива.
Пример 2.6.
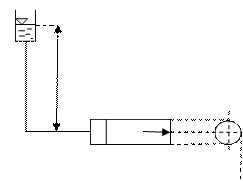
|
| Рисунок 2.11 - - Схема к примеру 2.6 |
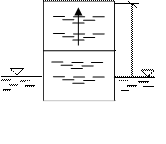
Определить давление жидкости на плоские боковые стенки цилиндрического резервуара, если его диаметр D=3 м (рисунок 2.10).
Решение:
Для этого сначала найдем силу давления Р (для избыточного давления).
Давление в центре тяжести площади стенки p = r g h = 9,81×1000×15 = 1,47×104, откуда:
P = pc w = pc p×d2/4 = 1,47×104×p×d2/4 = 1,03×105 Н.
Пример 2.7.
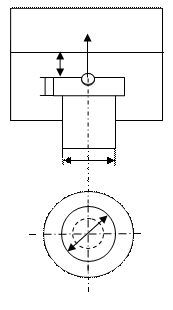 Рисунок 2.12 - - Схема к задаче 2.7 Рисунок 2.12 - - Схема к задаче 2.7
|
Определить усилие U, необходимое для того, чтобы поднять клапан (рисунок 2.11), если диаметр головки D = 0,5 м, диаметр цилиндрического ствола d = 0,3 м, высота головки а = 0,25 м и глубина погружения клапана h=1,25 м. Вес клапана G=29,4 H.
Решение. Необходимое усилие U находим из условия предельного равновесия
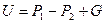 ,
,
где 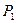 и
и 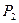 - силы давления жидкости на верхнюю и нижнюю (кольцевую)
- силы давления жидкости на верхнюю и нижнюю (кольцевую)
поверхности головки клапана. Вычисляем последовательно:
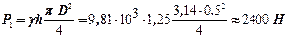
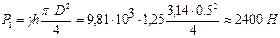
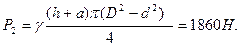
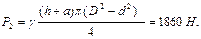
Искомое усилие 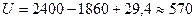 Н.
Н.
 Пример 2.8.
Пример 2.8.
| Рисунок 2.13 - - К задаче 2.8 |
Определить силу R давления жидкости на горизонтальное дно резервуара (внутреннее давление снизу вверх) в соответствии с рисуно 2.12, если 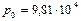 Па; d=2 м.
Па; d=2 м.
Решение:
Искомая сила R = p ω, где p - гидростатическое давление в центре тяжести площади ω (в точке М).
По формуле:
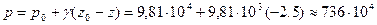
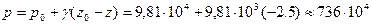 Па,
Па,
откуда
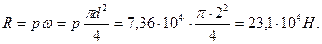
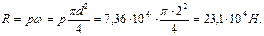
Пример 2.9.
Определить величину и направление силы гидростатического давления воды на 1 м. ширины вальцового затвора диаметром D = 1,5 м. (рисунок 2.13)
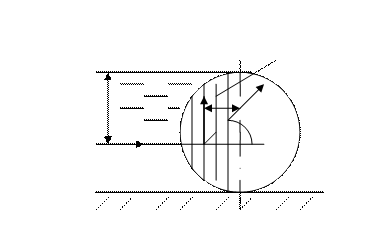 Рисунок 2.14-- К примеру 2.9 Рисунок 2.14-- К примеру 2.9
|
F l 
 yд
yд
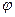 0
0
Решение:
Горизонтальная составляющая
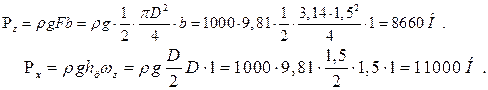 |
Вертикальная составляющая:
Суммарная сила давления:
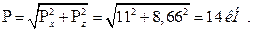 |
Составляющая Px проходит на расстоянии yд от свободной поверхности 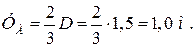
Составляющая Pz проходит на расстоянии l = 0,4244r от линии 1-1, равном 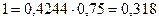 м.
м.
Равнодействующая P приложена в точке 0 под углом j к горизонту и проходит через центр круга.
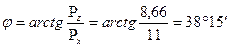
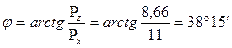
Задача 2.1
Стальная труба с внутренним диаметром D = 600 мм. работает под давлением р = 3 МПа. Найти : а) необходимую толщину стенок трубы , если допустимое напряжение для стали 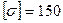 МПа ; б) максимально допустимое давление при толщине стенки трубы
МПа ; б) максимально допустимое давление при толщине стенки трубы 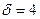 мм.
мм.
Ответ: а) 6 мм.; б) 2 МПа (20,4 кгс/см2). 3.Определить величину и направление силы давления воды на 1 м. ширины затвора (рисунок 3), если: а) R = 1 м.; Н = 2 м.; б) R = 2 м.; Н = 2,5 м..
Ответ: а) 22,9 кН ( 2,33 тс ); 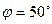 ; б) 50,1 кН (5,12 тс);
; б) 50,1 кН (5,12 тс); 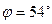 .
.
Задача 2.2
Найти силу давления воды на дно сосуда диаметром D = 1 м , если глубина H=0,7м, вес поршня G = 300 Н, d=0,5 м.
Ответ: 6,59 кН.
Задача 2.3
Наклонный прямоугольный щит плотины шарнирно закреплен на оси О. При каком уровне воды Н щит опрокинется, если угол наклона щита a=60°, а расстояние от его нижней кромки до оси шарнира d=1,3 м. Вес щита не учитывать.
Ответ: Н=3,38м.
Задача 2.4
Определить силу давления жидкости на торцевую плоскую стенку горизонтальной цилиндрической цистерны диаметром d=2,4 м, заполненной бензином плотностью r=760кг/м3, если уровень бензина в горловине находится на расстоянии H=2,7 м от дна. Цистерна герметически закрыта и избыточное давление на поверхности жидкости составляет 40 кПа. Найти также положение центра тяжести стенки..
Ответ: P=231 кН, Dl= 0,052 м.
Задача 2.5
Резервуар заполнен нефтью плотностью ρ=850 кг/м3 До высоты H=4 м . Избыточное давление на поверхности pн= 14,7 кПа. Определить реакции шарнира A и стяжного болта В крышки люка, если диаметр патрубка d=1м и его центр расположен на расстояниях H=1,5 м от дна резервуара, а=0,7 м и b=0,8 м. Вес крышки не учитывать.
Ответ: ra = 14.7 кН, rB = 13,4 кН.
Дата добавления: 2016-04-06; просмотров: 6646;