Сила давления жидкости на наклонную плоскую стенку

Представим на рисунок 2.4, а открытый сосуд, наполненный жидкостью и имеющий плоскую наклонную стенку ОМ. В плоскости этой стенки наметим оси координат Оу и Ох. Ось Ох направим перпендикулярно к плоскости чертежа.

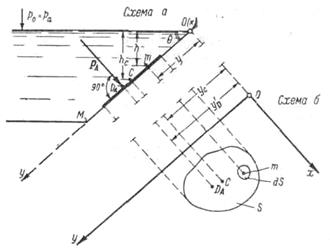Рисунок 2.7 - -Давление жидкости на плоскую наклонную фигуру площадью S

На стенке сосуда ОМ наметим некоторую плоскую фигуру любого очертания, имеющую площадь S. Эта фигура на рисунок 2.4, будет проектироваться в линию (показанную на чертеже жирно). Представим еще на рисунок 2-15, б стенку сосуда ОМ, повернутую относительно оси Оу на 90° (совмещенную с плоскостью чертежа). Ясно, что на рисунок 2.4 намеченная плоская фигура будет изображаться без искажения.

В соответствии с первым свойством гидростатического давления можем утверждать, что во всех точках площади S давление жидкости будет направлено нормально к стенке. Отсюда заключаем, что сила абсолютного гидростатического давления p_a, действующая на произвольную плоскую фигуру площадью S, будет также направлена по отношению к стенке нормально (как это показано на рисунок 2.4).

Поставим перед собой цель найти:

а) величину силы P_A абсолютного гидростатического давления;

б) положение линии действия силы P_A

Наметим на рассматриваемой фигуре произвольную точку т, заглубленную под уровнем жидкости на величину h и имеющую координату y, ясно, что

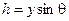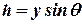
(2.44)

где q - угол наклона боковой стенки сосуда к горизонту.

У точки т выделим элементарную площадку dS Сила абсолютного гидростатического давления, действующая на эту площадку,

,

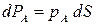(2.45)

или согласно (2-40)

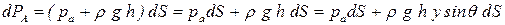
(2.46)

Интегрируя это выражение по всей площади S, получаем:

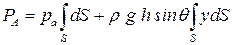
(2.47)

Ясно, что:

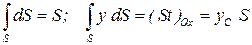
(2.48)

где (St)_0x - статический момент плоской фигуры относительно оси Ох;

у_С- координата центра тяжести (точки С) данной плоской фигуры.

Подставляя (2-79) в (2-78), получаем:

.

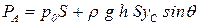(2.49)

Так как y_c sinq = h_c,

где h_c - заглубление центра тяжести C плоской фигуры под горизонтом жидкости, то

,

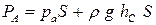(2.50)

или

,

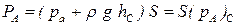(2.51)

где (P_A)_c -абсолютное гидростатическое давление в точке, являющейся центром тяжести рассматриваемой плоской фигуры.

Формулу (2.37) можно представить еще в виде:

,

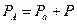(2.52)

здесь P_A - сила, обусловленная атмосферным (поверхностным) давлением, передающимся через жидкость на плоскую фигуру:

,

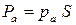(2.53)

P_c - сила избыточного (весового) давления:

,

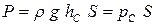(2.54)

где P_c - избыточное (весовое) давление в центре тяжести фигуры.

Как видно, сила гидростатического давления (абсолютного или избыточного), действующая на плоскую фигуру любой формы, равна площади этой фигуры, умноженной на соответствующее гидростатическое давление ((P_A)_c или P_c ) в центре тяжести этой фигуры.

Точка D_a пересечения линии действия силы P_A с плоскостью, в которой лежит рассматриваемая фигура, называется центром давления силы P_A. Найдем положение точки D_a, этим и определится линия действия силы P_A.