Дифференциальные уравнения равновесия жидкости

Выберем в покоящейся жидкости объём в виде параллелепипеда с ребрами, параллельными осям координат и размером Dx, Dy, Dz (рисунок 2.3). Рассмотрим силы, которые действуют на параллелепипед вдоль оси x. Массовые силы DF_x действуют на всю массу Dm и равны

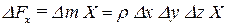
(2.29)

Поверхностные силы действуют на поверхность параллелепипеда. На левую и правую грань действуют нормальные напряжения (давление), поэтому, если известна площадь грани Dy Dz и давления на гранях эти силы будут равны:

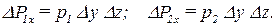
(2.30)

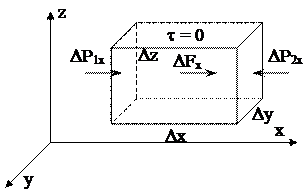Рисунок 2.3 - Вывод уравнения Эйлера гидростатики

Касательные напряжения должны действовать на боковые, относительно оси x, поверхности. Но так, как касательные напряжения возникают только при движении жидкости из-за сил трения, то они равны нулю. Запишем уравнение равновесия жидкости вдоль оси x

.

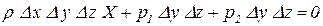(2.31)

Разделим последнее уравнение на массу параллелепипеда и устремим размеры параллелепипеда к нулю, тогда получим:

.

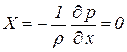(2.32)

Здесь мы воспользовались определением частной производной

.

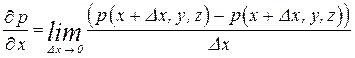(2.33)

Аналогично можно получить уравнения равновесия жидкости для осей y и z. Тогда полная система уравнений запишется:

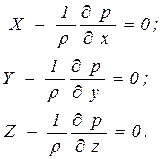
(2.34)

Умножим каждое из уравнения соответственно на dx, dy, dz и сложим их, тогда получим

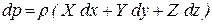
(2.35)

Последнее уравнение называется основным дифференциальным уравнением равновесия жидкости.