Основные физические свойства жидкости и газа.

Жидкостью называется физическое тело, обладающее большой подвижностью своих частиц и принимающих форму сосуда или части сосуда, в котором она находится.

Жидкости делятся на:

· слабо сжимаемые (капельные жидкости) – вода, нефть, керосин и другие;

· сжимаемые (газообразные жидкости) – воздух, кислород, метан.

С точки зрения физики, слабо сжимаемые жидкости это жидкости, а сжимаемые жидкости это газы. С точки зрения гидромеханики различие между ними заключается в разной зависимости плотности этих жидкостей от давления. Жидкости характеризуются следующими свойствами.

Плотностью жидкости ρ - называется отношение массы жидкости M к её объёму V

.

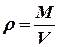(2.1)

Плотность жидкости в системе Си имеет размерность кг/м³.

Плотность воды при атмосферном давлении и температуре 4°С равна ρ_в = 1000 кг/м³.

Объёмным весом жидкости γ - называется отношение веса G жидкости к её объёму V

.

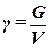(2.2)

Объёмный вес жидкости в системе Си имеет размерность н/м³.

Объёмный вес и плотность связаны между собой соотношением

.

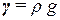(2.3)

С введением системы СИ объемный вес γ использовать в расчетных формулах запрещено. Но в старых учебниках и справочниках встречается понятия объемного веса, поэтому в этом случае необходимо перейти к плотности, используя соотношение (2.3).

Коэффициентом объёмного сжатия жидкости β_p – называется относительное изменение объема жидкости, при изменении давления на единицу

,

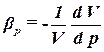(2.4)

где dV/V - – относительное изменение объёма жидкости;

dp - – изменение давления.

Коэффициент объёмного сжатия жидкости характеризует способность жидкости изменять объём, а соответственно и плотность, при изменении давления и в системе СИ имеет размерность Па^-1. Знак «минус» в формуле (2.2) выбран для того, чтобы коэффициент объёмного сжатия жидкости был положительным.

Модулем упругости жидкости Е_ж называется величина обратная коэффициенту объёмного сжатия жидкости:

,

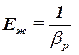(2.5)

Коэффициент объёмного сжатия и модуль упругости для воды соответственно равны β_p = 5 10^-10 Па^-1 и Е_ж = 2 10⁹ Па.

В водопроводных сетях давление составляет (0,3¸0,5) МПа. Поэтому даже при изменении давления равного Dp = 1 МПа относительное изменение объёма и плотности составит 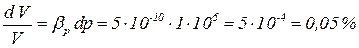, поэтому в этом случае можно считать плотность капельной жидкости постоянной ρ = ρ₀ =const.

При больших давлениях изменение объёма жидкости и плотности с давлением можно найти, интегрируя уравнение (2.4).

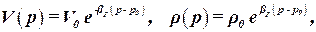
(2.6)

где V₀ и ρ₀ – объём и плотность жидкости при давлении p₀.

Коэффициентом температурного расширения жидкости β_t – называется относительное изменение объема жидкости, при изменении температуры на единицу

,

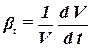(2.7)

где dV/V - – относительное изменение объёма жидкости;

dt - – изменение температуры.

Коэффициент температурного расширения жидкости характеризует способность жидкости изменять объём, а соответственно и плотность, при изменении температуры и в системе СИ имеет размерность 1/град.

Сжимаемые жидкости (газы) при малых изменениях давления и температуры также можно характеризовать коэффициентами объёмного сжатия и температурного расширения. Но при больших изменениях давлений и температур эти коэффициенты меняются в больших пределах, поэтому зависимость плотности идеального газа с давлением и температурой находятся на основе уравнения состояния Клайперона - Менделеева:

,

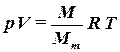(2.8)

где p – абсолютное давление, Па;

V – объём, который занимает газ, м³;

M – масса газа, кг;

M_m - молекулярная масса газа, кг/кмоль;

R = 8,314 Дж/моль·- универсальная газовая постоянная не зависит от состава газа;

T= 273,14 + t – абсолютная температура, K.

Разделим последнее уравнение на объём получим

,

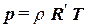(2.9)

где R’ = R/M_m – газовая постоянная зависит от состава газа.

Газовая постоянная для воздуха и метана соответственно равны , R΄_{воздуха} = 287 Дж/кг K˚; R΄_метан = 520 Дж/кг K˚.

Последнее уравнение иногда записывают в виде

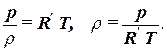
(2.10)

Из последнего уравнения видно, что плотность газа зависит от давления и температуры, поэтому если вам известна плотность газа, то необходимо указывать давление, температуру и состав газа, что неудобно. Поэтому вводятся понятия нормальных и стандартных физических условий.

Нормальные условия соответствуют температуре t = 0°С и давлению p_ат = 0,1013°МПа. Плотность воздуха при нормальных условиях равна ρ_в.н.ус = 1,29 кг/м³.

Стандартные условия соответствуют температуре t = 20°С и давлению p_ат = 0,1013°МПа. Плотность воздуха при стандартных условиях равна ρ_в.ст.ус = 1,22 кг/м³.

Поэтому по известной плотности при данных условиях, можно рассчитать плотность газа при других значениях давления и температуры

.

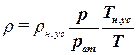(2.11)

Уравнение процесса. При движении газов происходит обмен теплом с окружающей средой, поэтому по разному меняется и плотность газа и давление и температура.

Изотермический процесс это процесс, при котором теплообмен с окружающей средой происходит мгновенно. Уравнение изотермического процесса записывается в виде:

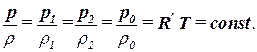
(2.12)

где p₁ – давление в начале процесса,

p₂ – давление в конце процесса,

p₀ – характерное давление, например при нормальных условиях.

Политропический процесс это процесс, при котором теплообмен с окружающей средой происходит, но затруднен. Уравнение политропический процесс записывается в виде:

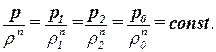
(2.13)

где n – показатель политропы.

Адиабатический процесс это процесс, при котором теплообмен с окружающей средой не происходит. Уравнение адиабатического процессапроцесс записывается в виде:

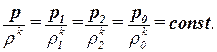
(2.14)

где k = c_p/c_v - показатель адиабаты;

c_p – теплоёмкость газа при постоянном давлении;

c_v – теплоёмкость газа при постоянном объёме.

Показатель адиабаты для воздуха k_возд. = 1,41, для метана k_метан = 1,31.

Вязкость жидкости.

Вязкостью называют свойство реальных жидкостей оказывать сопротивление движению слоёв жидкости друг относительно друга. Это свойство не может быть обнаружено при покое жидкости, так как оно проявляется лишь при ее движении.

Чтобы выяснить физическую сущность понятия вязкости, рассмотрим следующую схему. Пусть имеются слой жидкости толщиной y (рисунок 2.1). Нижний слой жидкости соприкасается с твердым телом и неподвижен. На верхнем слое находится твердая, невесомая пластина площадью w, к которой приложена сила T и поэтому она движется со скоростью u. При этом, как показывает опыт, промежуточные слои будут скользить один по другому со скоростью, пропорциональной их расстоянию до нижней пластинки.

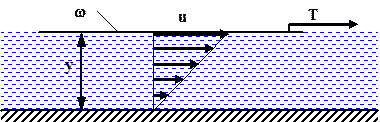Рисунок 2.1 - Пояснение свойства вязкости жидкости

Еще Ньютон высказал предположение, что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. Тогда сила, которую нужно приложить к пластинке, чтобы она двигалась со скоростью u, равна

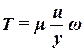
(2.15)

где μ - – коэффициент динамическая вязкость жидкости, зависит от рода жидкости.

Таким образом, вязкостью жидкости называетсявязкость есть физическое свойство жидкости, оказывать сопротивление движению слоёв жидкости друг относительно другахарактеризующее ее сопротивляемость скольжению или сдвигу.

Единицей измерения динамической вязкости является паскаль на секунду (Па·с) или мПа·с = 10^-3 Па·с. В справочниках встречаются старые единицы измерения динамической вязкости 1 пуаз = 1 г/см·с = 0,1 Па·с.

Динамическая вязкость воды зависит от температуры и может быть рассчитана по формуле

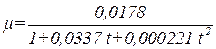
(2.16)

где μ - – кинематическая вязкость, Па·с;

t - – температура, °С.

Коэффициентом кинематической вязкости жидкости n называется отношение коэффициента динамической вязкости жидкости к плотности

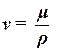
(2.17)

Единицей кинематической вязкости является квадратный метр на секунду (м²/с).

Вязкость различных сортов жидкости одного названия, например, нефти, в зависимости от химического состава и молекулярного строения может иметь различные значения.

Температурная зависимость вязкости нефти хорошо описывается формулой:

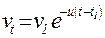
(2.18)

где n₁ - кинематическая вязкость нефти при температуре t₁,

u - коэффициент, который определяетсяустанавливаемый по экспериментальным данным.

Для определения коэффициента u необходимо знать вязкость нефти ν₁ и ν₂ при температуре t₁ и t₂

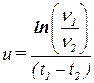
(2.19)

Вязкость жидкостей, как показывают опыты, зависят также от давления. При возрастании давления она обычно увеличивается.

Коэффициенты динамической и кинематической вязкости газов с повышением температуры увеличиваются.

Касательным напряжением t называется отношение силы действующей к поверхности касательно к величине площади этой поверхности w

.

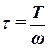(2.20)

Касательные напряжения имеют размерность давления (Па). Тогда закон Ньютона внутреннего трения в жидкости запишется

.

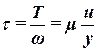(2.21)

Для линейной зависимости скорости координатой y касательные напряжения везде в потоке одинаковые. Если зависимость нелинейная, то формулу (2.15) необходимо записать для двух бесконечно близких пластинок:

.

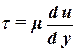(2.22)

Жидкость называется идеальной, если обладает следующими свойствами:

· абсолютно подвижна, μ = 0;

· абсолютно несжимаема, β_p = 0;

· не изменяет свой объём при изменении температуры β_t = 0,

Идеальной жидкости в природе нет, но есть типы движения жидкости, когда её можно считать идеальной.